第二章 随机变量及其分布
定义 随机变量 设随机试验的样本空间为 $ S= \lbrace e \rbrace$. $X=X(e) $ 是定义在样本空间 $ S $ 上 的实值单值函数. 称 $ X=X(e) $ 为随机变量.
与函数类比:
- 样本空间 $\rightarrow$ 函数的定义域
- 样本$e$ $\rightarrow$ 函数的自变量
- 实值单值函数$X$ $\rightarrow$ 函数关系
- 随机变量 $\rightarrow$ 函数值与函数的区别:
- 随机变量的取值随试验的结果而定,在试验之前不能预知它取什么值,
- 且它的取值有一定的概率.这些性质显示了随机变量与普通函数有着本质的差异.
离散型随机变量及其分布律
定义 离散型随机变量 全部可能取到的值是有限个或可列无限多个的随机变量
设离散型随机变量 $ X $ 所有可能取的值为 $ x_{k}(k=1,2, \cdots)$, $X$ 取各个可能值的概率, 即事件$\lbrace X=x_{k} \rbrace$ 的概率, 为
$$
P \lbrace X=x_{k} \rbrace = p_{k}, k=1,2, \cdots .
$$
由概率的定义, $ p_{k} $ 满足如下两个条件:
$$
\begin{aligned}
& 1^{\circ} \quad p_{k} \geqslant 0, k=1,2, \cdots ; \\
& 2^{\circ} \sum_{k=1}^{\infty} p_{k}=1 . \\
\end{aligned}
$$
$2^{\circ}$ 是由于 $\lbrace X=x_{1} \rbrace \bigcup \lbrace X=x_{2} \rbrace \cup \cdots$ 是必然事件, 且 $\lbrace X=x_{j} \rbrace \cap \lbrace X=x_{k} \rbrace
= \varnothing, k \neq j $,故 $ 1=P \left[ \bigcup_{k=1}^{\infty} \lbrace X=x_{k} \rbrace \right]=\sum_{k=1}^{\infty} P \lbrace X=x_{k} \rbrace \text {, 即 } \sum_{k=1}^{\infty} p_{k}=1 $.
(0 - 1)分布
设随机变量 $ X $ 只可能取 0 与 1 两个值, 它的分布律是
$$
P\lbrace X = k \rbrace = p^{k}(1-p)^{1-k}, k = 0,1 \quad (0<p<1),
$$
则称 $ X $ 服从以 $ p $ 为参数的 $ (0-1) $ 分布或两点分布. 其中$p$是取值为1的概率。
伯努利试验、二顶分布$X \sim b(n,p)$
设试验 $ E $ 只有两个可能结果: $ A $ 及 $ \bar{A} $, 则称 $ E $ 为伯努利 (Bernoulli)试验. 设 $ P(A)=p(0<p<1) $, 此时 $ P(\bar{A})=1-p $. 将 $ E $ 独立重复地进行 $ n $ 次, 则称这 一串重复的独立试验为 $ n $ 重伯努利试验。这里“重复”是指在每次试验中 $ P(A)=p $保持不变; “独立”是指各次试验的结果互不影响(放回抽样)。
由于各次试验是相互独立的, 因此事件 $ A $ 在指定的 $ k(0 \leqslant k \leqslant n) $ 次试验中发生, 在其他 $ n-k $ 次试验中 $ A $ 不发生(例如在前 $ k $ 次试验中 $ A $发生,而后$ n-k $次试验中$ A $不发生)的概率为
$$
\underbrace{p \cdot p \cdot \cdots \cdot p}{k \uparrow} \cdot \underbrace{(1-p) \cdot(1-p) \cdot \cdots \cdot(1-p)}{n-k \text { 个 }}=p^{k}(1-p)^{n-k} .
$$
这种指定的方式共有 $ \left(\begin{array}{l}n \ k\end{array}\right) $ 种, 它们是两两互不相容的, 故在 $ n $ 次试验中 $ A $ 发生 $ k $ 次 的概率为$ \left(\begin{array}{l}n \\ k\end{array}\right) p^{k}(1-p)^{n-k} $, 记 $ q=1-p $, 即有
$$
P \lbrace X=k \rbrace =\left(\begin{array}{l}
n \\
k \end{array}\right) p^{k} q^{n-k}, k=0,1,2, \cdots, n .
$$
当n = 1 时二项分布化为(0 - 1) 分布。
泊松分布
设随机变量 $ X $ 所有可能取的值为 $ 0,1,2, \cdots $, 而取各个值的概率为
$$
P \lbrace X = k \rbrace = \frac{ \lambda^{ k } \mathrm{ e }^{- \lambda }} {k !}, k=0,1,2, \cdots,
$$
其中 $ \lambda>0 $ 是常数. 则称 $ X $ 服从参数为 $ \lambda $ 的泊松分布, 记为 $ X \sim \pi(\lambda) $.
以$n,p $为参数的二项分布的概率值可以由参数为$\lambda = np$ 的泊松分布的概率值近似.
泊松定理 设 $ \lambda>0 $ 是一个常数, $ n $ 是任意正整数, 设 $ n p_{n}=\lambda $, 则对于任一固 定的非负整数 $ k $,有
$$
\lim {n \rightarrow \infty} \left(\begin{array}{l}
n \\\ k \end{array}\right) p{n}^{k}\left(1-p_{n}\right)^{n-k}=\frac{\lambda^{k} \mathrm{e}^{-\lambda}}{k !}
$$一般, 当 $ n \geqslant 20, p \leqslant 0.05 $ 时用$ \frac{\lambda^{k} \mathrm{e}^{-\lambda}}{k !}(\lambda= n p) $作为 $ \left(\begin{array}{l}n \ k\end{array}\right) p^{k}(1-p)^{n-k} $的近似值效果颇佳.
随机变量的分布函数
随机变量所取的值落在一个区间 $ \left(x_{1}, x_{2}\right] $ 的概率: $ P\lbrace x_{1}<X \leqslant x_{2} \rbrace $:
$$
P \lbrace x_{1}<X \leqslant x_{2} \rbrace =P \lbrace X \leqslant x_{2} \rbrace -P \lbrace X \leqslant x_{1} \rbrace,
$$
定义 设 $X$ 是一个随机变量, $x$ 是任意实数,函数
$$
F(x)=P \lbrace X \leqslant x \rbrace,-\infty<x<\infty
$$
称为 $X$ 的分布函数.
$F(x)$是取值在区间$[0,1]$的不减函数。
连续型随机变量的概率密度及其分布
对于随机变量 $X$ 的分布函数 $F(x)$, 存在非负函数 $f(x)$, 使对于任意实数 $x$ 有
$$
F(x)=\int_{-\infty}^{x} f(t) \mathrm{d} t,
$$
则称 $X$ 为连续型随机变量,其中函数 $f(x)$ 称为 $X$ 的概率密度函数, 简称概率密度。连续型随机变量的分布函数是连续函数. 在实际应用中遇到的基本上是离散型或连续型随机变量。由定义知道,概率密度 $f(x)$ 具有以下性质:
$1^{\circ} f(x) \geqslant 0$;
$2^{\circ} \int_{-\infty}^{\infty} f(x) \mathrm{d} x=1$;
$3^{\circ}$ 对于任意实数 $x_{1}, x_{2}\left(x_{1} \leqslant x_{2}\right)$,
$$
P \lbrace x_{1}<X \leqslant x_{2} \rbrace =F\left(x_{2}\right)-F\left(x_{1}\right)=\int_{-x_{1}}^{x_{2}} f(x) \mathrm{d} x,
$$
$4^{\circ}$ 若 $f(x)$ 在点 $x$ 处连续, 则有 $F^{\prime}(x)=f(x)$.
概率密度的定义与物理学中的线密度的定义相类似, 这就是为什么称f位)为概率密度的缘故.
若不计高阶无穷小,有: $ P \lbrace x< X \leq x+ \Delta x \approx f(x) \Delta x \rbrace $
均匀分布 $X \sim U(a,b)$
若连续型随机变量 $\mid X$ 具有概率密度
$$
f(x)= \begin{cases}\frac{1}{b-a}, & a<x<b, \ 0, & \text { 其他, }\end{cases}
$$
称 $X$ 在区间 $(a, b)$ 上服从均匀分布. 记为 $X \sim U(a, b)$.
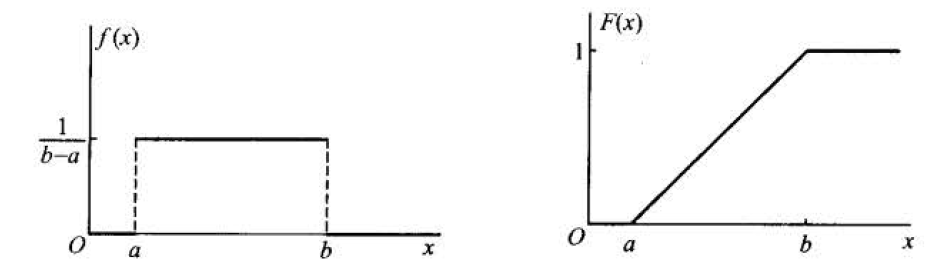
概率密度函数下方的总面积为1,因为面积代表概率,而概率是必须为1。
指数分布
若连续型随机变量 $X$ 的概率密度为
$$
f(x)= \begin{cases}\frac{1}{\beta} \mathrm{e}^{-x / \beta}, & x>0, \ 0, & \text { 其他, }\end{cases}
$$
其中 $\theta>0$ 为常数, 则称 $X$ 服从参数为 $\theta$ 的指数分布.
累积分布函数为:
$$
F(x ; \beta)=\lbrace \begin{array}{cl}
1-e^{- \frac{1}{\beta} x} & , x > 0 \\
0 & , x<0
\end{array} .
$$
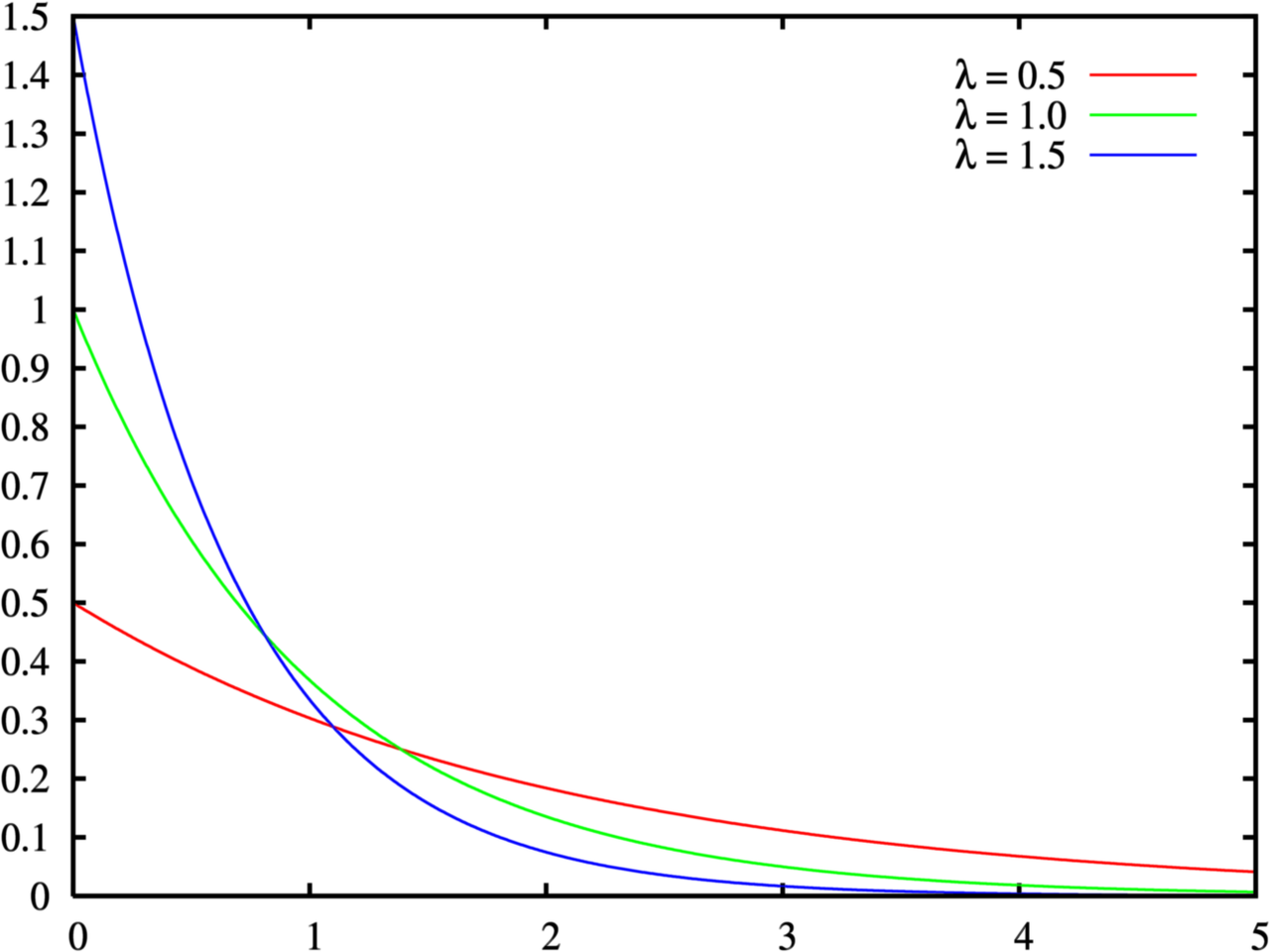
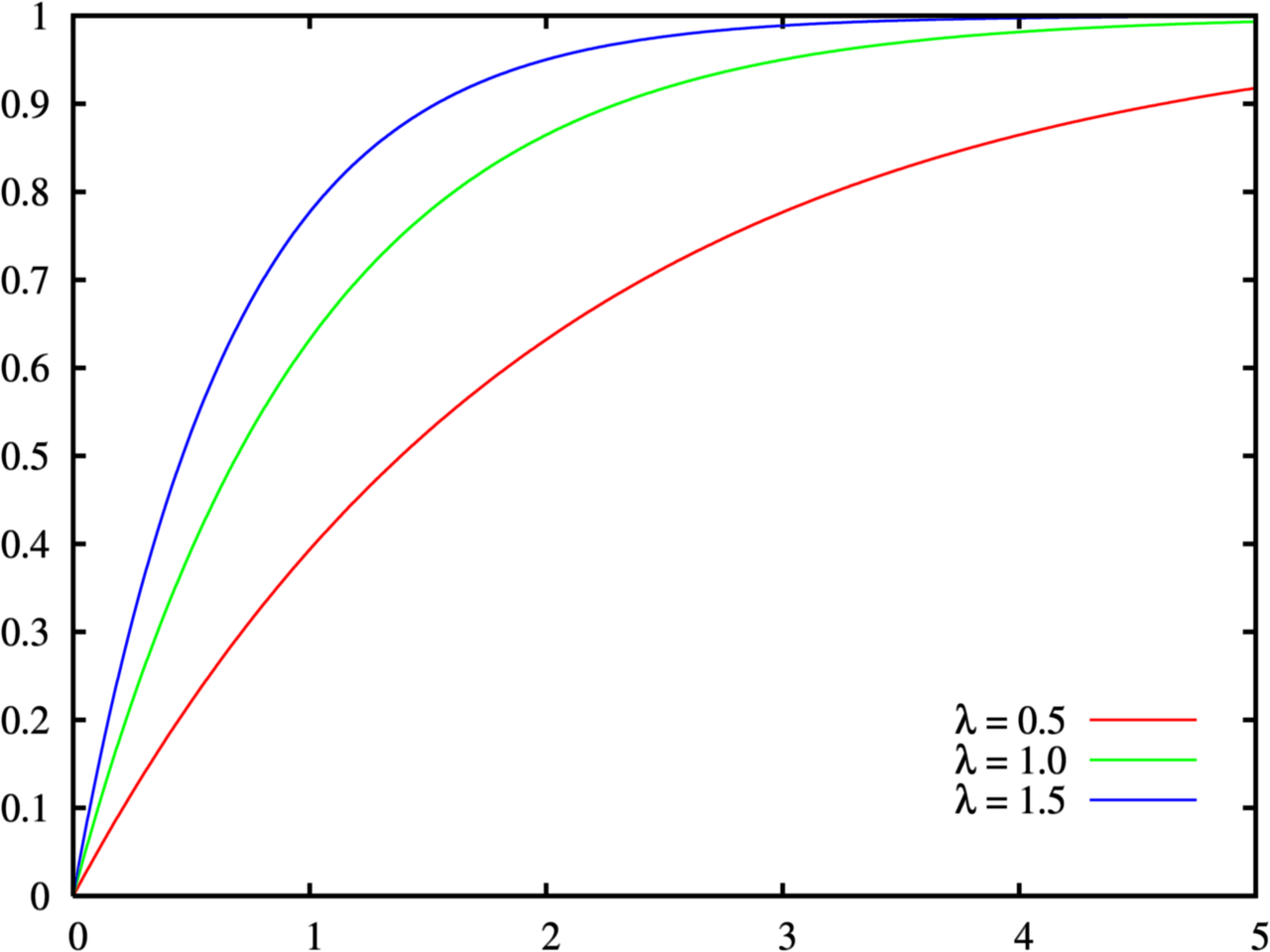
无记忆性特点需要理解
正态分布/高斯分布$X \sim N\left(\mu, \sigma^{2}\right)$
若连续型随机变量 $X$ 的概率密度为
$$
f(x)=\frac{1}{\sqrt{2 \pi \sigma}} \mathrm{e}^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}},-\infty<x<\infty,
$$
其中 $\mu, \sigma(\sigma>0)$ 为常数, 则称 $X$ 服从参数为 $\mu, \sigma$ 的正态分布或高斯 (Gauss) 分布, 记为 $X \sim N\left(\mu, \sigma^{2}\right)$.
特别, 当 $\mu=0, \sigma=1$ 时称随机变量 $X$ 服从标准正态分布. 其概率密度和分 布函数分别用 $\varphi(x), \Phi(x)$ 表示, 即有
$$
\begin{gathered}
\varphi(x)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-t^{2} / 2}, \\
\Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} \mathrm{e}^{-t^{2} / 2} \mathrm{~d} t .
\end{gathered}
$$
其中:
$$
\Phi(-x) = 1-\Phi(x)
$$
一般, 若 $X \sim N\left(\mu, \sigma^{2}\right)$, 我们只要通过一个线性变换就能将它化成标准正态 分布.
引理 若 $X \sim N\left(\mu, \sigma^{2}\right)$, 则 $Z=\frac{X-\mu}{\sigma} \sim N(0,1)$.

Comments 1 条评论
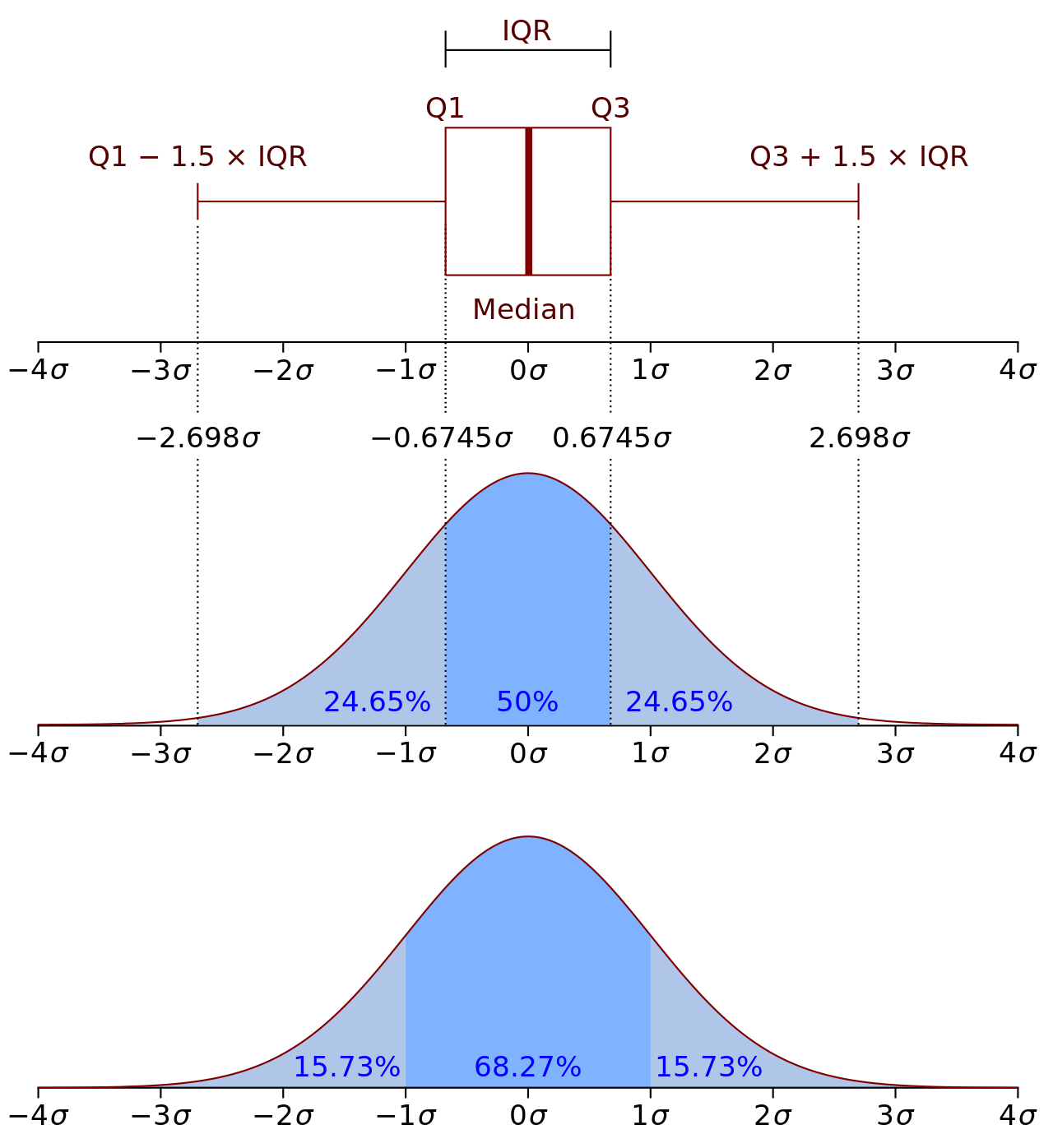
正态分布中“$\sigma$原则”、“2$\sigma$原则”、“3$\sigma$原则”分别是:
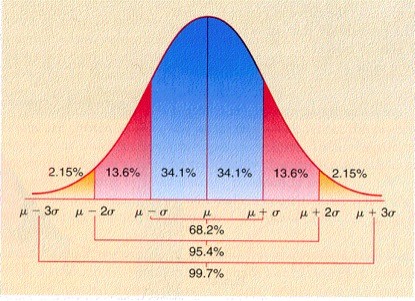
$\sigma$原则:数值分布在(μ-σ,μ+σ)中的概率为0.6826;
2$\sigma$原则:数值分布在(μ-2σ,μ+2σ)中的概率为0.9544;
3$\sigma$原则:数值分布在(μ-3σ,μ+3σ)中的概率为0.9974;