奇异值分解
Singular Value Decomposition,SVD在一般线性代数中多有提及,应用范围甚广,尤其是机器学习中常用的主成分分析(PCA)中关键的步骤。SVD可以将任何矩阵分解为三个特别的矩阵,不论其对称性,形状和秩的大小(no restrictions on: Symmetry,Dimension,Rank)。
$A=U\sum V^{T}$
$\Sigma$是一个矩形对角矩阵(rectangular diagonal),对角线上的数字是矩阵A的奇异值,而且按照降序排列,其他所有元素都是零,奇异值表示在各个轴上的伸缩变换情况。V和U都是正交矩阵(orthogonal),U矩阵包含了A的左奇异矩阵$S_{L}$的归一化特征向量,这些特征向量按照特征值的降序排列。V矩阵包含了A的右奇异矩阵$S_{L}$的归一化特征向量,这些特征向量同样按照特征值的降序排列。
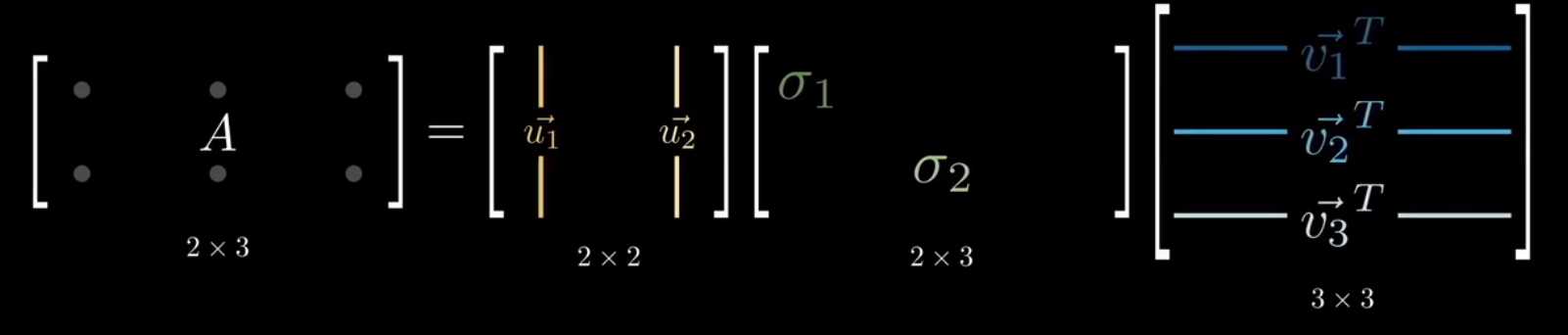
以二维矩阵为例进行说明:
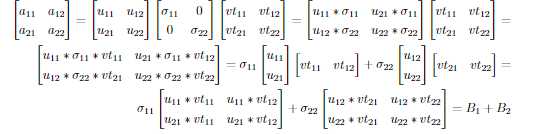
更常规的写法为:
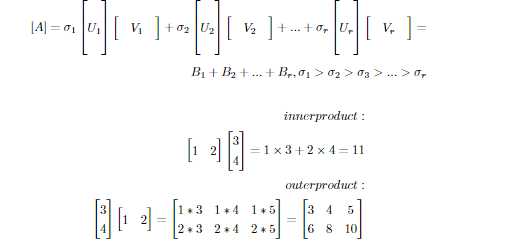
注意:$n\geq r$,r为矩阵的秩,具体可参考:矩阵的奇异值分解,图像压缩
将任意一个矩阵A分解,选取其中奇异值较大的矩阵,图像压缩中常用此矩阵代替原矩阵($A \approx B_{1}+B_{2}+...+B_{k}$),所取得奇异值对应矩阵的数目k越多,则保留的图像信息越多。
Python中实现SVD
import numpy as np
S = np.zeros([5,5])
A=np.random.randint(1,25,[5,5])
u,sigma,vt = np.linalg.svd(A)
print('Original Matrix:',A)
for i in range(5):
S[i][i] = sigma[i]
print('Recovered Matrix:',np.dot(np.dot(u,S),vt))
注意:python中的svd分解得到的VT就是V的转置,Python中svd后得到的$\Sigma$是一个行向量,Python中为了节省空间只保留了A的奇异值,所以我们需要将它还原为奇异值矩阵。同时需要注意的是,比如一个55大小的矩阵的奇异值只有两个,但是他的奇异值矩阵应该是55的,所以后面的我们需要手动补零,并不能直接使用diag将sigma对角化。
必备知识
矩阵向量乘法
一个大小为m x n 的矩阵有能力将n维向量变换为m维的向量,换一种说法就是矩阵在$R^{n}$和$R^{m}$之间施加了一个线性变换。例如:
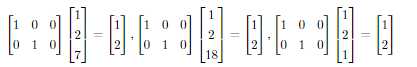
这个矩阵就代表了从欧式空间$R^{3}$到$R^{2}$变换的一个简单形式,它与任何向量的乘积都只会保留x和y,无论初始的z是多少,由于乘数为0最后都会完全抹去z。z这就意味着,我们可以把$R^{3}$中所有形如$[1,2,z]$的向量都映射为$[1,2]$。我们将这个矩阵称为维度消除器(dimension eraser),其会剔除掉第三维的信息,而对角矩阵会对x轴和y轴进行一定比例的拉伸,比例取决于数值大小。
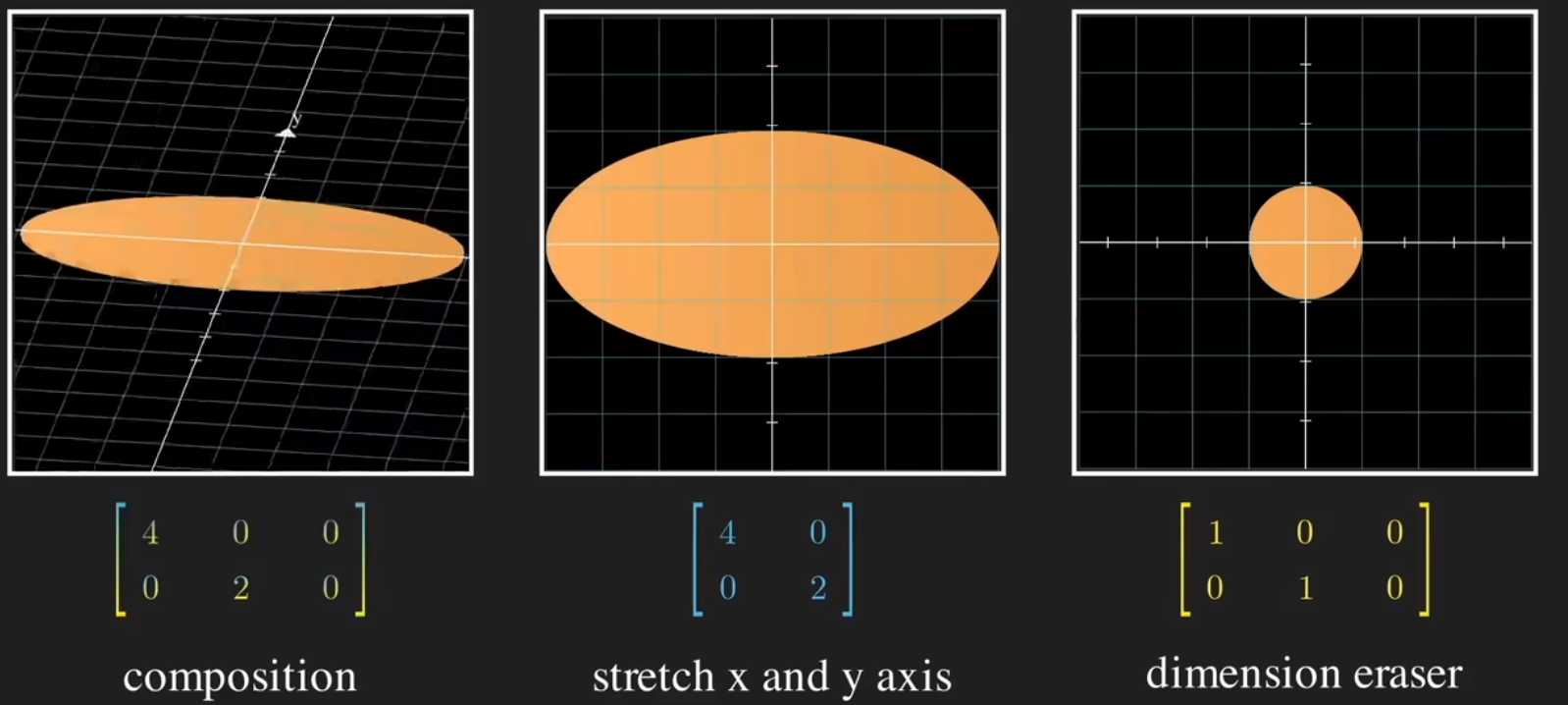
同理也会有矩阵可以增加向量维度,例如下面这个例子:
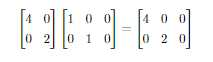
对称矩阵

非退化矩阵
非退化矩阵 (non-degenerate matrix) 又称“非异矩阵 (non-singular matrix) ”、“满秩矩阵”,若 n 阶矩阵 A 的行列式 |A|≠0,则称 A 为一个非退化 矩阵,若 |A|=0,则称 A 为“退化矩阵”,也称“奇异矩阵”、“降秩矩阵”。n阶方阵 A 是非退化的充要条件为 A 是可逆矩阵。非退化可以视为“线性无关的刻画”。若对给定的矩阵 A, 如果存在矩阵 B,使得 AB= BA= I, 则称A为非退化矩阵,并称矩阵 B 为矩阵 A 的逆矩阵 (inverse matrix); 非退化矩阵因此也称为可逆矩阵 (invertible matrix) 或非奇矩阵 (non-singular matrix)。

• 非退化矩阵的行列式不为零,即矩阵可逆
• 如果 A 是非退化阵,则其逆阵是惟一的, 由于可逆阵 A 的逆阵为惟一
确定,故可记之为 A−1,有 AA−1 \= A−1A \= I
• 方阵 A,B,若 AB=I,则必 BA=I
• 单位阵必为非退化阵,且其逆阵即为自身
• 退化矩阵就是不可以被对角化的矩阵,因为它的特征向量个数少于特
征值个数。

Comments NOTHING