Blacklock等人(2012)描述了使用新型的马尔可夫链算法生成1D丝束基因座。在这项研究中,我们采用相同的算法来生成3D丝束表示,将增广马尔可夫链算法与拓扑规则相结合以消除通过蒙特卡罗方法生成随机3D物体时不可避免出现的互穿或其他排序错误,将其转换为物理上有效的虚拟样本。
在本研究中,提出了简单且普遍适用的拓扑排序规则,并开发了在概率丝束结构生成器中实现这些规则的程序。与以往消除丝束相互渗透的方法不同,该程序不需要进行形变计算并且完全基于纺织品的几何形状的经验数据,因此不需要了解纺织品的加工历史或其本构特性。相反,可以使用两种广泛适用的排序算法来表示拓扑排序规则,这两种算法在没有外部干预的情况下同时执行,从而可以预测出接触区的形状。
下面是该程序的详细过程:
1. 离散
截面的形状选择是一个灵活的因素,椭圆形状只是一种合理但并非必需的选择,所以实验数据或最终生成的截面形状并不需要接近椭圆形。虽然在3D生成器中引入椭圆来表示纤维束截面但是它们也可以是矩形或其他形状,并且随着生成步骤的进行即由于拓扑规则、调整和平滑操作等步骤的影响,截面形状可能会发生变化而不再保持椭圆形状。
纤维束的生成是通过对每个截面进行离散化来完成的。这是通过在x-y平面上定义的一个公共矩形网格{(Xi,Yj),i=1,2,...,Nx,j=1,2,...,Ny}上表示所有属的每根纤维束来实现的。因此,例如在经向纤维束沿着x轴名义对齐的编织结构中,纤维束m由连续的网格行i上的一组截面定义,每个截面都是一组坐标对:
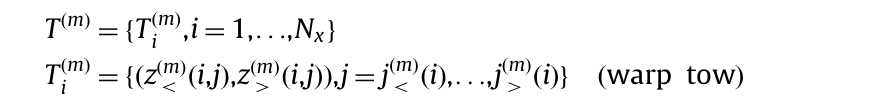
其中,$z_{}^{(m)}(i,j)$定义了在网格点(i,j)处的丝束的下表面和上表面;并且$j_{}^{(m)}(i)$是丝束在网格行i上的截面上所占据的网格索引j的最小值和最大值。类似的定义适用于纬向纤维,行i和列j互换。
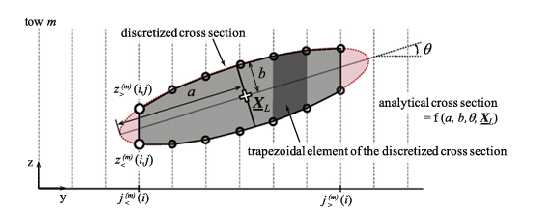
沿纤维束轴垂直的网格平面上的纤维束m的一个截面。在离散网格上,初始的椭圆形截面由四边形的串联表示。在消除纤维束之间的排序错误过程中,椭圆形轮廓会进一步偏离。
2. Z/$\rho $-排序
上述描述的生成步骤被重复以创建所有纤维束。由于生成的纤维束中的非随机周期性变化基于数据并且往往比随机偏差要大,因此生成的纺织品副本往往与实验测得的纺织品一致。特别的,纤维束会根据需要向上、向下和向侧移动以避免相互交织时的碰撞。然而由于每个纤维束都遵循自己的生成算法所规定的轨迹,没有详细检查它相对于其他纤维束的位置,因此纤维束相互穿插或纤维束的部分序列错误的情况可能发生。这些情况违反了纺织品的拓扑规则。因此,生成副本的下一步是系统地消除所有拓扑错误的情况。这通过应用一对校正算法来实施排序规则来实现的,一个用于平面内的$^{\cdot}\rho $-ordering规则$O^{(\rho)}$,另一个用于z-ordering规则$O^{(z)}$。通过对问题进行矩形离散化,应用校正算法变得简化。
2.1 Z-排序
z方向(通过厚度)上的顺序被指定为逻辑表达式的数组$O(z)$,任何丝束对m和n的排序可以取以下三个值:
$$
O_{mn}^{(z)}=\begin{cases}Z_m\geq Z_n&\text{if }\Omega_m\neq\Omega_n\text{ and }m\text{ above }n\\Z_m\leq Z_n&\text{if }\Omega_m\neq\Omega_n\text{ and }m\text{ below }n\\{indeterminate}&\text{if }\Omega_m=\Omega_n\end{cases}\quad(m=1,\ldots,N_t;n=1,\ldots,N_t)
$$
其中$\Omega_{m}$是丝束m所属的属,$Z_{m}$表示由丝束m沿z轴占据的区间,“高于”或“低于”分别表示向正或者负Z方向进行。$Z_{m}\geq Z_{n}\text{或}Z_{m}\leq Z_{n}$仅在丝束m和丝束n之间的交叉处强制执行,不要求丝束m处处占据比丝束n处处占据更高或更低的z值。条件“不确定”意味着在任何位置都有可能对丝束m和n进行任何排序。在同一属的丝束确实重叠的情况下(例如经线丝束的平行边缘)如果也存在不同属的丝束,则可以间接确定它们的排序,因为它们可能都是相对于该位置的第三根丝束排序的。但是如果没有第三根丝束介入,则可能发生任何排序。
排序只能在成对丝束之间指定,通常不可能对所有丝束建立单一的排序。例如$z_{m}>z_{n}\mathrm{and}z_{n}\geq z_{p}$这一事实并不意味着$z_{m}\geq z_{p}$。
对于平纹组织,z排序如下图a所示。
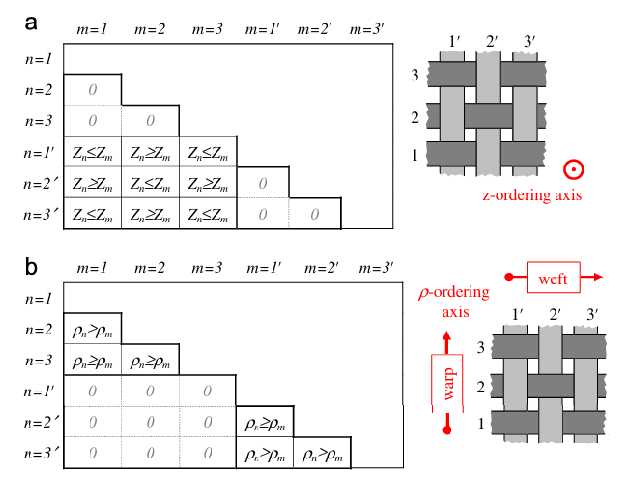
2.2 平面内排列($\rho $排列)
平面内方向(x–y平面)上的顺序被指定为逻辑表达式$O^{(\rho)}$的第二个数组,其中任何一对丝束i和j的排序取以下三个可能值之一:

其中,$\rho $轴(x轴或y轴)垂直于给定属的丝束轴的主平面内方向,$\rho_{m}$表示丝束m沿$\rho $轴占据的区间,“右”或“左”分别表示向$\rho $的较高或较低值移动。$\rho_{m}\geq\rho_{n}$或$\rho_{m}\leq\rho_{n}$仅在垂直于$\rho $轴的平面上的两个丝束的投影彼此交叉的情况下实施,不要求丝束m处处占据比丝束n处处占据更高或更低的$\rho $值。下图显示了两种可能违反$\rho $排序的例子,即“交叉(crossing)”和“亲吻(kissing)”。对于平纹组织,$\rho $有序阵列的元素如图(b)所示。
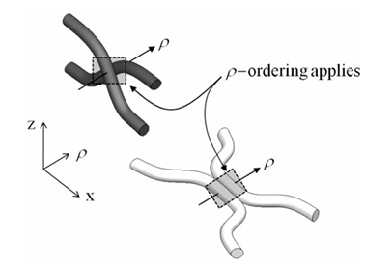
任何纺织品的拓扑结构可以由其排序数组$O^{(z)}\mathrm{and}O^{(\rho)}$来定义。
2.3 排序符号
假设丝束m和n在它们都占据的网格点$(i,j)$处占据间距$Z_{m}=[z_{}^{(m)}(i,j)]\mathrm{and}Z_{n}=[z_{}^{(n)}(i,j)]$。当比较两个丝束在z方向上的排序时,可以区分三种排序状态:
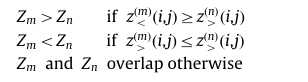
关于第三种状态,在应用排序算法时,不需要区分不同的可能重叠情况。可用于具有相同或不同属的丝束对。
3. 消除渗透-强制执行拓扑顺序
3.1 边缘后退算法
网格平面上同一属的两根丝束的截面通常表现出相对位置的几种典型情况。假设丝束m和n的排序规则是$\rho_{m}<\rho_{n}$。在丝束n的三个图示位置中,位置1和3满足排序规则,而位置2违反了排序规则,因为它涉及互穿。位置3不违反$^{\cdot}\rho $排序,因为即使沿$^{\cdot}\rho $轴的间隔$\rho_{m}$和$\rho_{n}$重叠,重叠也发生在两个丝束在z轴上的投影分离的地方。因此,丝束相互悬垂,这是同一属丝束的常见且拓扑上可容许的变化。
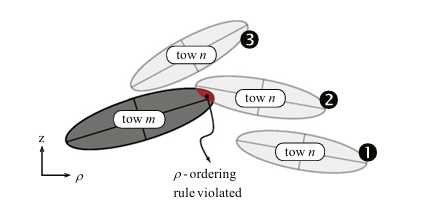
对于同一属的每对丝束m和n,每次对满足以下条件之一的所有行应用边缘后退校正:
(i) 第i行上任何j的间隔$[z_{}^{(m)}(i,j)]\mathrm{and}[z_{}^{(n)}(i,j)]$都重叠。
(ii) 丝束 m和n在行i上共享公共网格点,并且在行i上任何点j处的间隔$[z_{}^{(m)}(i,j)]\mathrm{and}[z_{}^{(n)}(i,j)]$的排序不同于在行i+1或行i-1上任何点j0处间隔$[z_{}^{(m)}(i\pm1,j^{\prime})]\mathrm{and}[z_{}^{(n)}(i\pm1,j^{\prime})]$的排序,其中排序的差异是通过考虑上述排序(2.3)中定义的三种状态来确定的。
下面应用边缘后退算法来消除同一属的丝束对间的相互渗透。
- 取同一属的任何一对丝束m和n。考虑两个经向丝束的例子,它们名义上与x轴对齐。首先,沿着x方向进行扫描,搜索两个丝束的截面的相互穿透。当网格点$(i,j)$处丝束在z方向上占据的间隔$[z_{}^{(m)}(i,j)]\mathrm{and}[z_{}^{(n)}(i,j)]$。网格第i行上的典型互穿情况如下图a所示。
- 边缘后退算法消除网格行i的j重叠,直到极限点
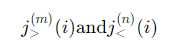 相等,并且剩余丝束截面服从排序$\rho_{m}\leq\rho_{n}$。网格点i的j值被选择为其旧值的平均值($\Bigg(j_{>}^{(m)}(i)-j_{<}^{(n)}(i)\Bigg)/2$),如果必要,则转移到下一个更高的整数值。在一个方向上一致地进行偏移可以最小化得到的纱线几何形状的粗糙度。
相等,并且剩余丝束截面服从排序$\rho_{m}\leq\rho_{n}$。网格点i的j值被选择为其旧值的平均值($\Bigg(j_{>}^{(m)}(i)-j_{<}^{(n)}(i)\Bigg)/2$),如果必要,则转移到下一个更高的整数值。在一个方向上一致地进行偏移可以最小化得到的纱线几何形状的粗糙度。
在网格的第i行应用边缘后退步骤后,为两个丝束留下一个共同的j值,被标记为共同点或者"纤维束对接点"。在对接点处,两个丝束在z方向上占据的区间不需要相同(图(b))。
边缘后退算法得到的接触平面始终平行于z轴,这与相同属丝束之间相互穿插倾向于发生两种交叉配置(crossing和kissing)之一的事实一致即沿其边缘压入接触的纤维束倾向于形成大致平行于z轴的平坦接触表面。
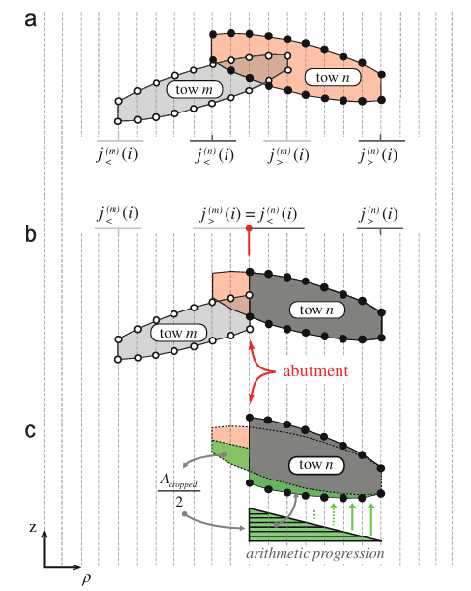
(a) 边缘后退之前。 (b) 边缘后退之后,剩余的共同网格点被标记为两个纤维束之间的对接点。(c) 经过线性变化扩张后重新塑造的纤维束以保持截面积不变。
3.2 Z排序算法
通过一次对一个网格点(i,j)应用以下z排序算法来消除不同种类的丝束之间的相互渗透。
在任何多重占用的网格点上,存在一组由纤维束集合$S_{ij}={m_{1},m_{2},m_{3},...}$占据的间隔$[z_{}^{(m_{1})}(i,j)],[z_{}^{(m_{2})}(i,j)],[z_{}^{(m_{3})}(i,j)],\ldots,$。在典型的工程纺织品中,占据网格点的纤维束数量可能从零到10不等,这取决于纺织品的结构。这些纤维束的所需z轴排序由排序数组$O^{(z)}$指定。z轴排序算法包括将在z方向上位于单个网格点(i,j)移动间隔$[z_{}^{(m_{1})}(i,j)],[z_{}^{(m_{2})}(i,j)],\cdots,$以确保遵守占据网格点的所有纤维束对的已知排序。
在$O^{(z)}$中的排序规则适用于不同属丝束的纤维束对,而相同属丝束的纤维束对的排序是不确定的。如果$S_{\mathrm{i}j}$ 中的所有纤维束属于不同的属,它们之间的逐对排序为该网格点上的唯一整体排序。(在 $S_{\mathrm{i}j}$中出现冲突的逐对排序的情况几乎从不发生。它们需要同一纤维束的多个不同部分共同占据一个网格点,这只有在纤维束的横截面上具有凹入特征的情况下才可能发生。然后这种凹入特征在示例材料中从未见过。)
对于真实的输入数据,在$S_{\mathrm{i}j}$中发现的任何一个属的丝束都不超过两个。当一个属的两个丝束包含在$S_{\mathrm{i}j}$中时,它们的相对顺序是不确定的,除非$S_{\mathrm{i}j}$中存在不同属的丝束,并且该丝束的顺序在其中一个丝束的上方而在另一个丝束的下方。
可以通过以下步骤更正Z-排序错误:
(1) 在$S_{\mathrm{i}j}$上执行成对搜索以识别排序错误中涉及的所有丝束。然后将这些丝束收集到$S_{\mathrm{i}j}$的子集中,表示为$S_{ij}^{(p)},p=1,\ldots,$并且定义为使得任何子集内的丝束彼此呈现排序误差,但不与不在该子集中的任何丝束呈现排序误差。这种分离将校正过程分解为处理例如靠近区段顶部的丝束和靠近底部的丝束的校正。
(2) 然后在每个子集内执行排序校正,调用$O^{(z)}$。
- 如果$S_{ij}^{(p)}$不包含两个相同属的丝束,则$S_{ij}^{(p)}$排序的结果是唯一的。
-
如果$S_{ij}^{(p)}$包含两个相同属的丝束,则在$S_{ij}^{(p)}$中必然也至少存在一个不同属的丝束(否则就不会有排序错误)。如果另一个这样的丝束被排序在相同属对中的一个之上和另一个之下,则通过调用$O^{(z)}$进行排序的结果是唯一的。但是,如果不同属的所有丝束的排序高于或低于同一属的两个丝束,则同一属对的排序仍然是不确定的。在这种情况下,它们相对于彼此的顺序保持不变。
(3) 步骤(2)的结果是$S_{ij}^{(p)}$中丝束的修订排序,表示为索引整数的有序列表。为了完成排序校正,对于正确排序并相互接触的所有$m\in S_{ij}^{(p)}$,必须在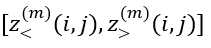 上为丝束分配新的区间(共享共同的z区间边界)。
上为丝束分配新的区间(共享共同的z区间边界)。
(4) 在分配了新的间隔之后,在两个不同的子集$S_{ij}^{(p)}$之间可能出现新的重叠。通过使两个重叠的集合成为单个集合并重新应用步骤(1)-(3),利用快速收敛来消除这些。
4. 几何形状的调整
丝束的横截面积对局部纤维堆积密度起着决定性作用,从而对局部性能、载荷分布和失效机制产生重要影响。在进行Z排序和边缘后退校正之后,丝束的横截面积可能会发生变化。然而,由于排序错误校正也会对丝束的截面纵横比和方向产生变化,但通常这种变化是适度的。此外,这些变化对于失效机制的影响往往次于横截面积变化所引起的失效。因此,为了消除Z排序和边缘后退校正对丝束性能的影响,需要对丝束的横截面积进行调整,以保持丝束在经过排序和校正后的横截面积恒定。
4.1 边缘撤退后丝束横截面的调整
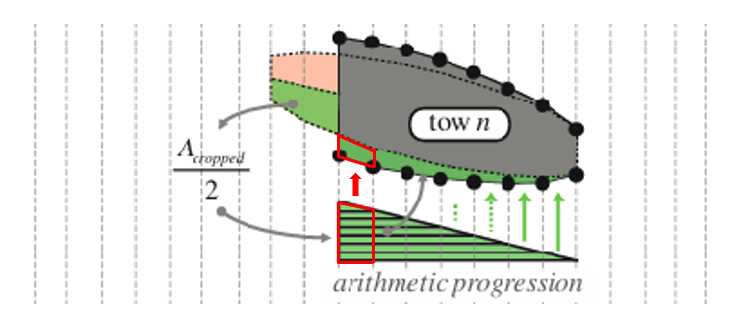
在边缘后退算法的应用过程中,丝束横截面的面积和纵横比可能会发生变化。为了保持丝束横截面积,丝束在z方向上扩张。扩张因子从丝束边缘处相对较大值的线性减小,丝束边缘已退回到远边缘的单位值。选择扩张因子的大小以保持丝束的横截面积。图中补偿的直角三角形面积为由于边缘后退损失的丝束横截面积的一半,三角形的底边是$j_{>}^{(n)}(i)-j_{<}(i)$,其中$j_{<}(i)$是新生成的纤维束对接点处的j值。这个直角三角形的高可以根据面积和底边算出,也就是补偿到丝束横截面上第一个梯形的下底,这个梯形的面积与三角形中位置相同处的梯形面积相等。所以丝束横截面的第一个梯形的上底可以根据这个梯形的面积、高和下底来计算出,第一个梯形的上底为第二个梯形的下底。以此类推可以得到丝束所有梯形的上下底,从而就可以补偿到丝束的横截面上。同样的方法补齐丝束横截面上方的区域。
4.2 Z排序后丝束横截面的调整
考虑$n_{p}$个具有相互排序误差的丝束的子集$S_{ij}^{(p)}$。在重新排序之后,由丝束沿着z轴占据的间隔${[[z_{}^{(m)}(i,j)],m\in s_{ij}^{(p)}]}$,被重新定义,使得:
(1) 间隔是连续的,即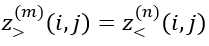 ,其中m和n是校正顺序中的连续间隔。
,其中m和n是校正顺序中的连续间隔。
(2) 每个间隔的长度,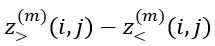 ,不变。
,不变。
(3) 间隔的质心不变,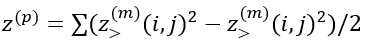 ,其中和是在$S_{ij}^{(p)}$上得出的。
,其中和是在$S_{ij}^{(p)}$上得出的。
在此调整之后,$S_{ij}^{(p)}$实际上由长度为$\sum z_{>}^{(m)}(i,j)-z_{>}^{(m)}(i,j)$的单个区间组成以$z^{(p)}$为中心。$S_{ij}^{(p)}$中连续的所有丝束对标记为在网格点$\left(i,j\right)$处接触。
上述程序的优点是丝束的任何部分的面积保持不变(因为定义丝束的间隔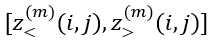 保持恒定),而丝束截面质心的变化(在所有丝束截面上平均)被最小化(因为在Z方向上占据任何网格点的所有丝束的质心保持恒定)。
保持恒定),而丝束截面质心的变化(在所有丝束截面上平均)被最小化(因为在Z方向上占据任何网格点的所有丝束的质心保持恒定)。
(在这里存在疑问点:可以通过以下三种方式调整丝束来消除丝束对在Z方向上的相互渗透。
平移调整:对于相邻的丝束可以通过平移它们的横截面来消除在Z方向上的重叠或干涉。这可以通过调整丝束的位置来实现。
缩放调整:如果需要调整丝束之间的间距或相对尺寸,可以对丝束的横截面进行缩放调整。这可以通过增加或减少丝束的尺寸来实现使得它们适应所需的排列方式。
旋转调整:在某些情况下可能需要对丝束进行旋转调整以便它们在Z方向上能够消除渗透。通过将丝束绕其轴线旋转一定角度,可以实现丝束之间的最佳排列。
文中提到了每个丝束间隔的长度保持不变,所以排除缩放调整。若为平移调整,丝束的质心应该会发生变化。所以在这里是都采取的旋转调整吗?如果都是采取旋转调整是否会存在一些情况导致不管旋转多少度纤维束对仍然相互渗透?是否可以根据渗透情况来采取不同的措施。)
不同属丝束的接触情况如下所示。第一种情况是接触纱线在两侧都改变位置,第二种情况是接触纱线仅在一侧改变位置,第三种情况是接触纱线在任一侧都不改变位置。第1和第2种情况与接触纱线相交,而第3种情况没有相交。

对于第一种情况,采用平移调整。对于第二种情况,采用旋转调整。转角度θ的计算公式如下:$\theta=tan^{-1}\left(\frac{h}{2s}\right)$,其中H是纤维束的高度即$z_{>}^{(m)}(i,j)-z_{<}^{(m)}(i,j)$,s是纤维束间距(即两个相邻同属纤维束质心的距离)。

5. 平滑
样本生成器算法中存在三种导致物理上不现实的纤维束边界不规则性的来源。第一种是马尔可夫链算子,其可以在任意随机变量${\xi^{(m)},z^{(m)},A^{(m)},ar^{(m)},\theta^{(m)}}$的偏差中引入网格相关的小波长振荡。第二种是在${x,y}$平面中使用离散网格,其在丝束的横向边界(在${x,y}$平面上的投影中看到的边界)中引入台阶。后者的不规则性通过使用边缘后退算法来校正$\rho$-排序错误而加剧。第三个是在校正z排序误差的过程,其可在互穿区域的边缘处留下丝束的z坐标中的梯度,所述梯度大于丝束中的纤维可遵循的梯度。
所有这些类型的不规则性都具有与在问题的离散化中选择的网格大小大致相称的空间波长。网格尺寸应远小于丝束的宽度,因此远小于所有相关长度,这些相关长度往往近似等于或大于丝束宽度(或交叉之间的距离)。因此,可以通过应用平滑操作来去除不规则性,而不会损害发生器的保真度。在平滑操作中,应用Blacklock等人提出了一种改进的平均算法,该算法倾向于保留偏差的RMSD。
5.1 Z-平滑
由马尔可夫链算子产生的不规则性的平滑可以通过在随机丝束变量的生成之后立即进行单个平滑操作来去除,然后对丝束进行离散化或应用排序校正。
随后通过修改后的平均算法实现由于Z-排序校正引起的不规则性的平滑。平滑仅沿着经向丝束应用,而不在纬向丝束方向上应用。因为经向丝束的连续性可以提供平滑度的特征而纬向丝束的不规则性与纤维-纤维剪切有关,并且这种不规则性在真实样品中观察到,应该保留在模型中。
5.2 XY-平滑
最后对离散网格引起的不规则性进行平滑处理,需要为不在网格上的丝束边缘上的点引入x和y坐标。这种平滑必须在丝束生成中的所有其他步骤完成之后进行。为了确保不引入新的相互渗透,丝束边缘上的新点必须位于丝束的现有体积内。
此外,可以通过网格效应最小化来减小离散网格造成的面积损失。
当模型离散化时和在排序校正过程中,丝束轨迹和形状特征会发生较小的波动。虽然沿着丝束的面积随位置的变化不受生成程序的影响,但面积始终移动到略微减小的值。面积损失主要发生在离散化过程中并且与椭圆形状在椭圆占据的最后网格点处的截断有关。
这种离散化的影响可以通过修改椭圆试验截面的离散化方式来避免,通过(1)每当椭圆的极值比椭圆占据的最后一个点更靠近下一个网格点时,将横截面延伸到该点(即有时向上取整所占据的网格点的数量而不是总是向下取整),以及(2)修改丝束截面的顶部和底部表面的指定z值,以确保面积守恒。使用第一种修改而不仅仅是第二种修改确保了纵横比变化的最小化。
离散化的第二个影响是在丝束的边缘引入了台阶。为了减小这种影响,可以通过网格细化最小化来消除台阶的存在,但是这样做会减少计算处理的样本数量。一种优选的方法是在后处理过程中,通过在位于网格点之间的丝束表面上引入新的点,随后对丝束进行平滑处理。为了确保不引入新的排序错误,这些新点可以被限制在未修改的纤维曲面的体积内。
6. 迭代的可能必要性
纤维束截面形状的排序校正、平滑步骤和调整原则上可以改变丝束的统计数据。如果使用目标统计数据作为输入,则它们可能与生成的虚拟样本的统计数据不匹配。如果差异很大,则需要一个迭代过程,修改输入统计信息直到输出统计信息达到目标。

Comments NOTHING