Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------
Definitions
Marginal Probability: Probability of an event, irrespective of any other event
P(X), P(Y)
Conditional Probability: Probability of an event, given another event is already true.
\begin{gathered}
P(X \text { given } Y), P(Y \text { given } X) \
P(X \mid Y), P(Y \mid X)
\end{gathered}
Joint Probability: Probability of multiple events occurring together.
\begin{gathered}
P(X \text { and } Y), P(Y \text { and } X) \
P(X \cap Y), P(Y \cap X) \
P(X, Y), P(Y, X)
\end{gathered}
General Form for Conditional Probability?
\mathrm{P}(\mathrm{C} \mid \mathrm{B}, \mathrm{A})=\frac{P(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})}{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}
Recall:
P(B \mid A)=\frac{P(A \cap B)}{P(A)}
Substitute:
\mathrm{P}(\mathrm{C} \mid \mathrm{B}, \mathrm{A})=\frac{P(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})}{\mathrm{P}(\mathrm{B} \mid \mathrm{A}) \mathrm{P}(\mathrm{A})}
Reorganize:
P(A \cap B \cap C)=P(C \mid B, A) P(B \mid A) P(A)
General Form, Recursion of Conditionals
\mathrm{P}\left(A_{1} \cap \cdots \cap A_{n}\right)=\mathrm{P}\left(A_{n} \mid A_{n-1}, \ldots, A_{1}\right) \mathrm{P}\left(A_{n-1} \mid A_{n-2}, \ldots, A_{1}\right) \ldots \mathrm{P}\left(A_{1}\right)
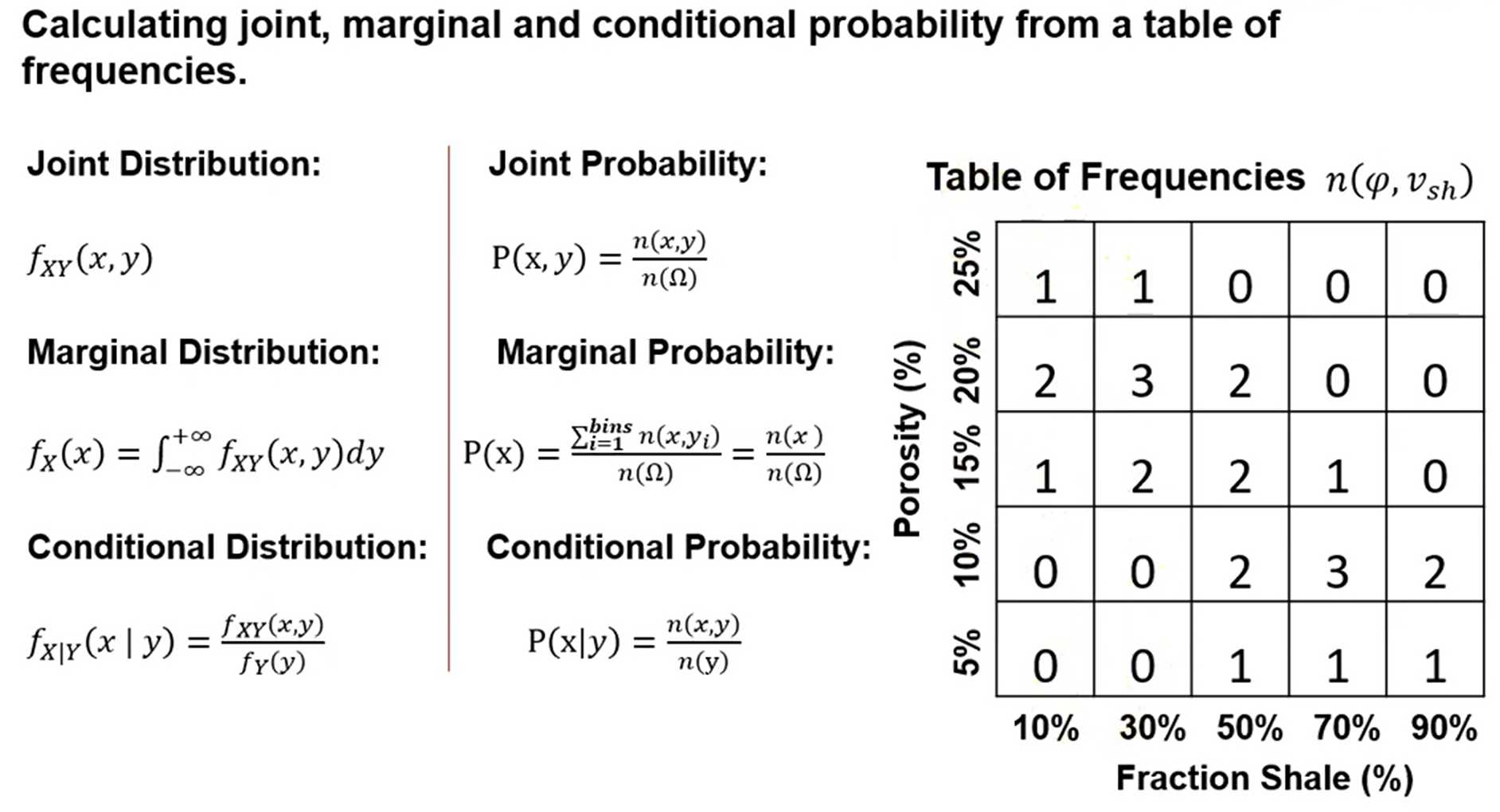
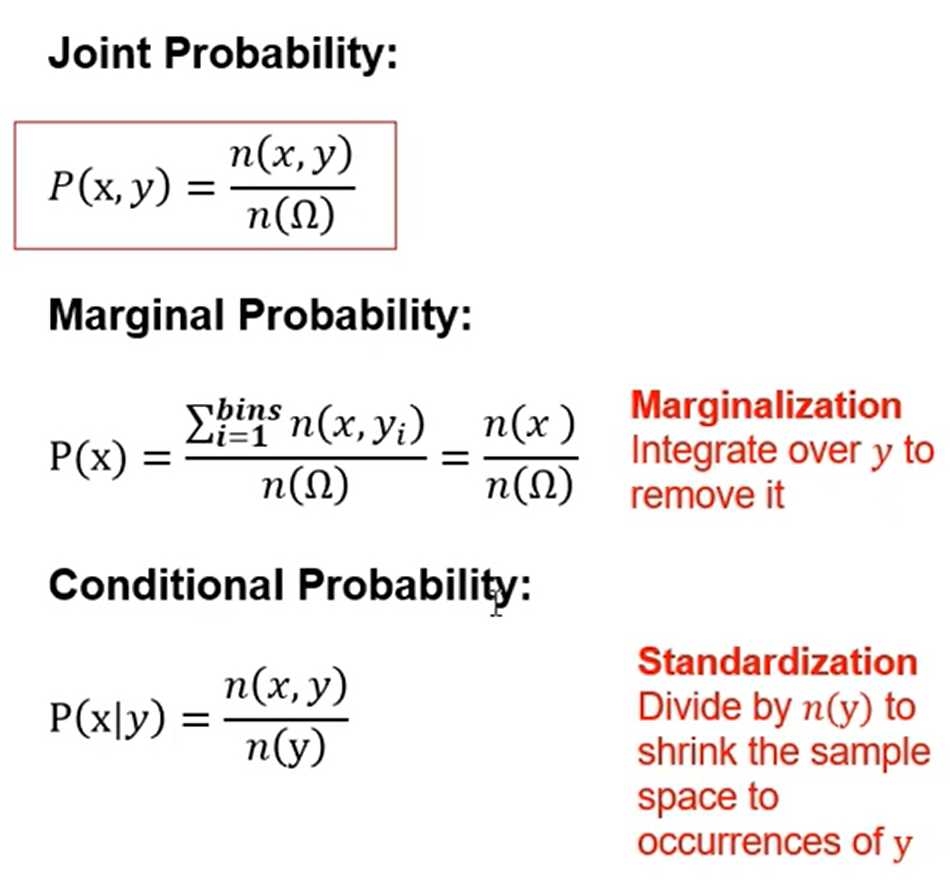
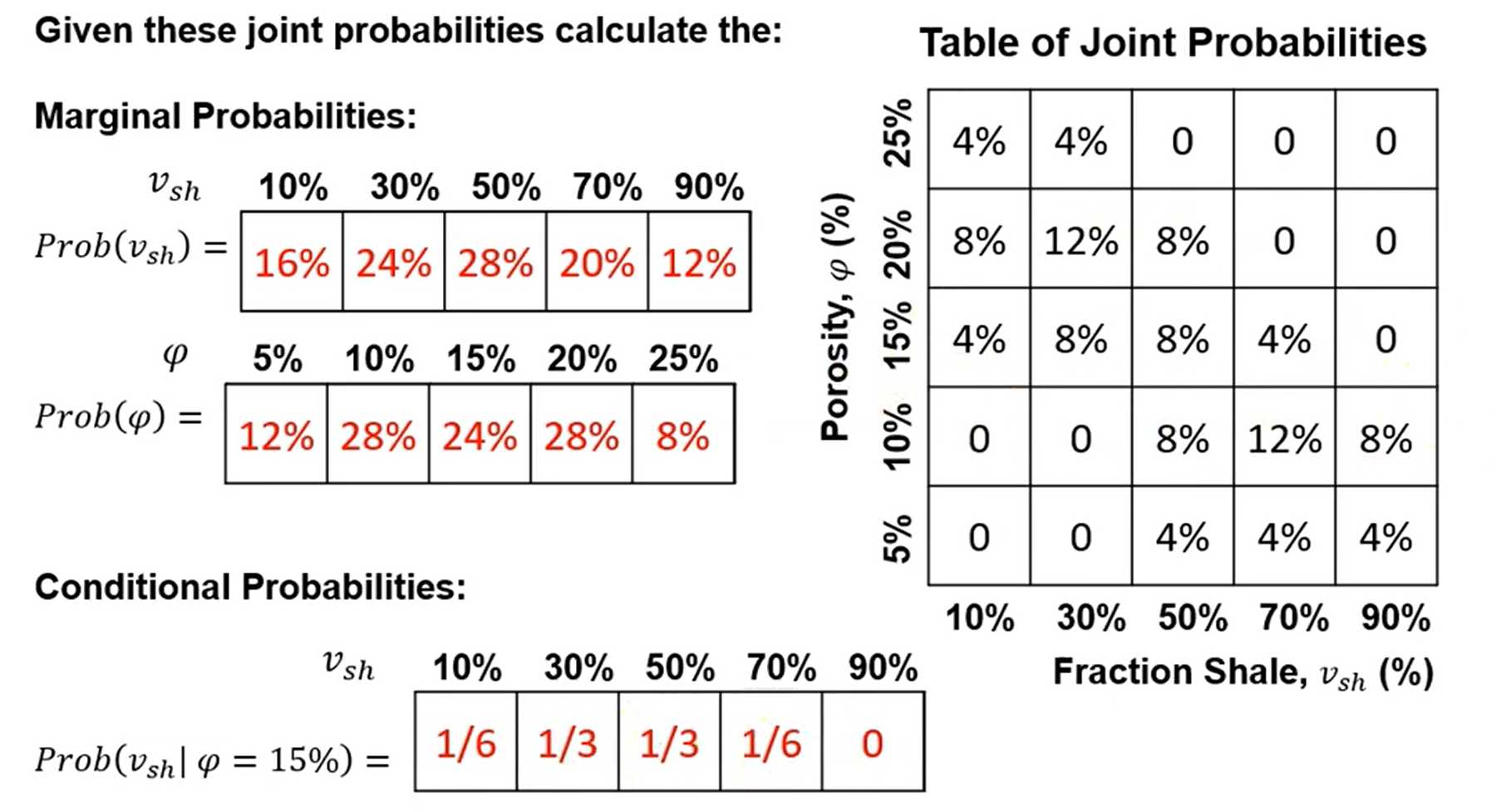
Calculating joint, marginal and conditional probability from a table of frequencies.
The Multiplication Rule
\mathrm{P}(A \cap B)=\mathrm{P}(\mathrm{B} \mid \mathrm{A}) \mathrm{P}(A)
If events A and \mathbf{B} are independent:
\mathrm{P}(B \mid A)=\mathrm{P}(\mathrm{B})
Knowing something about A does nothing to help predict B. Then by substitution:
\mathrm{P}(A \cap B)=\mathrm{P}(\mathrm{B}) \mathrm{P}(A)
The general form given independence for all cases, i=1, \ldots, k :
\begin{gathered}
P\left(\bigcap_{i=1}^{k} A_{i}\right)=\prod_{i=1}^{k} P\left(A_{i}\right) \
\text { e.g. } P\left(A_{1} \cap A_{2} \cap A_{3}\right)=P\left(A_{1}\right) P\left(A_{2}\right) P\left(A_{3}\right)
\end{gathered}
Events A and B are independent if and only if:
\begin{gathered}
\mathrm{P}(A \cap B)=\mathrm{P}(\mathrm{B}) \mathrm{P}(A) \
\text { or } \
\mathrm{P}(A \mid B)=\mathrm{P}(A) \text { and } \mathrm{P}(B \mid A)=\mathrm{P}(\boldsymbol{B})
\end{gathered}
Recall the General Form:
Events A_{1}, A_{2}, \ldots, A_{n} are independent if:
\mathrm{P}\left(\cap_{i=1}^{k} \mathrm{~A}_{\mathrm{i}}\right)=\prod_{i=1}^{k} \mathrm{P}\left(\mathrm{A}_{\mathrm{i}}\right)
Comments NOTHING