马尔科夫链及转移矩阵简单案例及Python实现

发布于 2023-06-16  1559 次阅读

Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------

一、马尔科夫链和转移矩阵的介绍

created: 2023-06-16T18:01:20 (UTC +08:00)
tags: [马尔科夫链转移矩阵怎么求]
source: https://blog.csdn.net/m0_45161766/article/details/107235866

1、马尔科夫链(Markov chain)概述

机器学习算法中，马尔可夫链在时间序列模型广泛的应用。主要思想是不管初始状态是什么，只要状态转移矩阵不发生变化, 最终状态始终会收敛到一个固定值, 这种无记忆性叫马尔科夫属性。公式为：

P(xt+1∣…,xt−2,xt−1,xt)=P(xt+1∣xt)\mathrm{P}\left(\mathrm{x}_{\mathrm{t}+1} \mid \ldots, \mathrm{x}_{\mathrm{t}-2,} \mathrm{x}_{\mathrm{t}-1}, \mathrm{x}_{\mathrm{t}}\right)=\mathrm{P}\left(\mathrm{x}_{\mathrm{t}+1} \mid \mathrm{x}_{\mathrm{t}}\right)

2、转移概率矩阵(Transition Probability Matrix)

转移概率矩阵： 矩阵各元素都是用概率表示。其值非负，并且各行元素之和等于1。在一定条件下是互相转移的，故称为转移概率矩阵。 例如：矩阵AA某一位置aij)a_{ij})的值为P(j∣i)P(j|i),即从状态ii转化到状态jj的概率，如状态转移矩阵为：

A=[0.90.0750.0250.150.80.050.250.250.5]A=\left[\begin{array}{ccc}0.9&0.075&0.025 \\0.15&0.8&0.05 \\0.25&0.25&0.5\end{array}\right]

3、马尔科夫链形成过程

给定初始状态如：p0=[0.5,0.2,0.3]p_0=[0.5, 0.2, 0.3], kk步转化过程为：p0=p0∗pkp_0=p_0*p_k。计算机程序需要利用迭代变量，借助循环实现。二步转移概率矩阵正好是一步转移概率矩阵的平方。kk步转移概率矩阵是一步转移概率矩阵的kk次方。$k$步转移概率矩阵中,各行元素之和也都为1。 经过多步转化p0p_0收敛于固定值(稳态)。本实例为[0.6248219,0.31266282,0.06251528][ 0.6248219, 0.31266282, 0.06251528]。

二、举例说明

1、问题描述

根据上述基本原理，用python程序验证马尔科夫链形成过程：两个初始状态 p01=[0.5,0.2,0.3]p_{01}=[0.5, 0.2, 0.3], p02=[0.1,0.4,0.5]p_{02}=[0.1,0.4,0.5]; 状态转移矩阵都为AA;

A=[0.90.0750.0250.150.80.050.250.250.5]A=\left[\begin{array}{ccc}0.9&0.075&0.025 \\0.15&0.8&0.05 \\0.25&0.25&0.5\end{array}\right]

经过k(30)k(30)步完成马尔科夫链转化过程。 要求完成转化过程计算并将其过程与结果用图形表示。

2、代码实现

相比原文进行了代码完善。 

import numpy as np
import matplotlib.pyplot as plt


def calanddraw(p0, p, ax, c, n):
    """
    Calculate and draw the probability distribution of the Markov chain:
      p0 -> p0 * p -> p0 * p * p -> ...

    Parameters
    ----------
    p0 : array_like
        Initial probability distribution.
    p : array_like
        Transition matrix.
    ax : matplotlib.axes._subplots.AxesSubplot
        Axes on which to plot.
    c : list
        A list of colors for plotting.
    n : int
        Number of iterations.

    Returns
    -------
    None
    """
    # Draw the initial probability distribution
    for j in range(len(p0)):
        ax.scatter(0, p0[j], c=c[j], s=2)

    for i in range(n):
        # Calculate the probability distribution of step i
        p0 = np.mat(p0) * np.mat(p)

        # Draw the probability distribution of step i for each state
        for j in range(len(np.array(p0)[0])):
            ax.scatter(i+1, p0[0, j], c=c[j], s=2)  # 确定画点属性


if __name__ == '__main__':
    """ Make up some data for Markov chain analysis """
    # Initial probability distribution. The sum of each row is 1.
    p01 = np.array([0.5, 0.2, 0.3])
    p02 = np.array([0.1, 0.4, 0.5])

    # Transition matrix. The sum of each row is 1.
    A = np.array([[0.9, 0.075, 0.025],
                  [0.15, 0.8, 0.05],
                  [0.25, 0.25, 0.5]
                  ])

    """ Calculate and draw the probability distribution of the Markov chain """
    n = 30  # Iteration times
    c = np.array(['r', 'g', 'b'])  # Color of each state

    fig = plt.figure(figsize=(15, 6))
    ax1 = fig.add_subplot(121)
    ax2 = fig.add_subplot(122)

    calanddraw(p01, A, ax1, c, n)
    calanddraw(p02, A, ax2, c, n)
    plt.show()
Python

3、运行结果

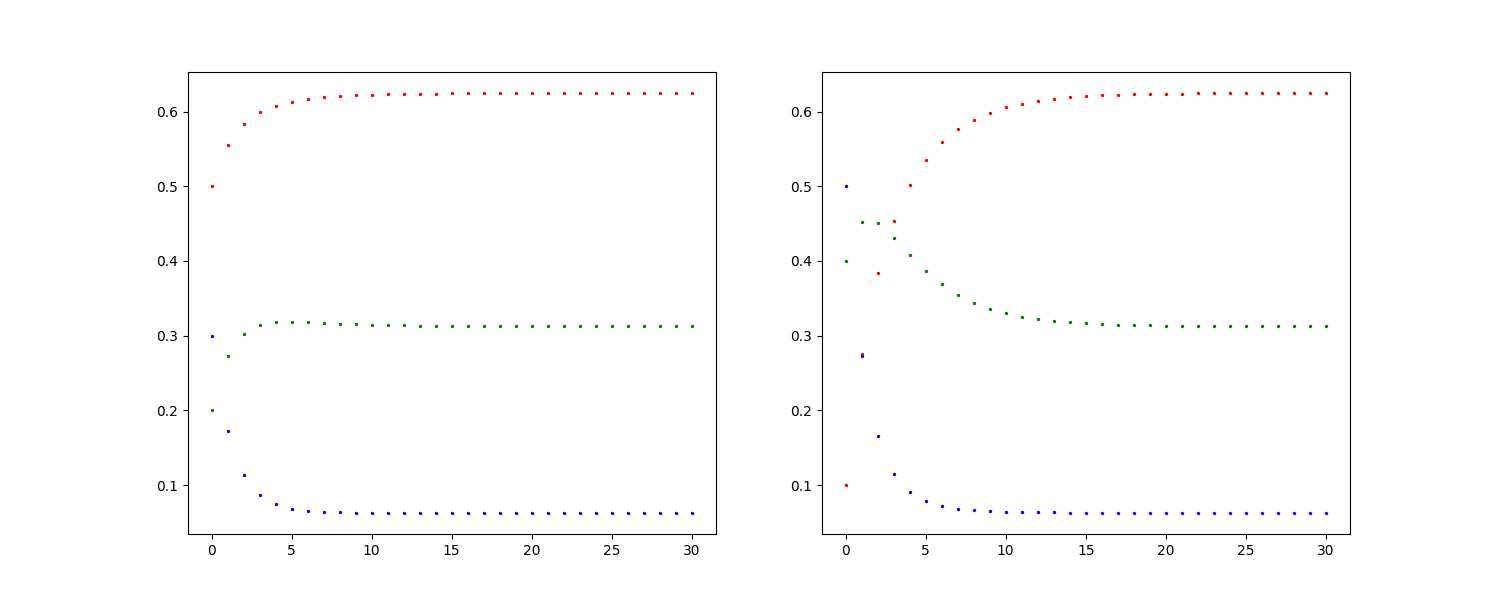
如下图所示，两个初始状态的不同的三个初始值（初始状态），经过相同的状态转移矩阵完成马尔科夫链转化后，不仅数值本身收敛，而且两组收敛值趋于相同：


两组不同初值的马尔科夫链转化过程图

Everything not saved will be lost.
最后更新于 2023-06-16
啥也没有呀
  1. 一、马尔科夫链和转移矩阵的介绍
    1. 1、马尔科夫链(Markov chain)概述
    2. 2、转移概率矩阵(Transition Probability Matrix)
    3. 3、马尔科夫链形成过程
  2. 二、举例说明