To do:
1. 整理并上传文档,内容包括12步的公式推导、基本方法、代码及其解析、CFD基础知识、目前在其中遇到的问题
2. 分清楚动态粘度和动力学粘度
12 Steps to Navier-Stokes
Intro
通过12个步骤,掌握最基本的CFD方法。
原教程出处:CFD Python: 12 steps to Navier-Stokes :: Lorena A. Barba Group (lorenabarba.com)
1. CFD基础知识介绍(待完善)
1.1 流体力学控制方程组
CFD无论具有什么形式,都是建立在流体力学基本控制方程——连续性方程、动量方程、能量方程之上的,它们分别基于对应的三个基本物理学原理:质量守恒定律、牛顿第二定律、能量守恒定律。这些方程具有各种不同的形式,同一个算法往往只能求解特定形式的方程,因此对于CFD而言,理解这些不同形式的方程,尤其是其对应的物理意义很重要。
1.2 流动模型
对于有流动性的流体,有四种流动模型,基于它们可以导出四种不同形式的控制方程,这些控制方程本质上为同一个方程
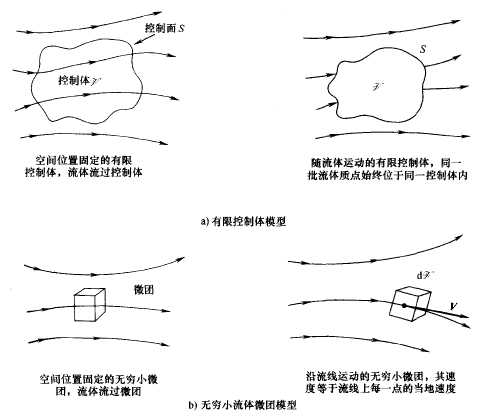
| 有限控制体 | 无穷小流体微团 | |
|---|---|---|
| 守恒型控制方程 | 空间位置固定 | 空间位置固定 |
| 非守恒型控制方程 | 随流体流动 | 随流体流动 |
1.3 控制方程组导出
1.3.1 基本概念
- 物质导数 $frac{D}{Dt}$
物质导数:$frac{D}{Dt}equivfrac{partial}{partial t}+(vec{V}cdotnabla)$
速度向量场:$vec{V}=uvec{i}+vvec{j}+wvec{k}$
哈密顿算子:$nablaequivvec{i}frac{partial}{partial x}+vec{j}frac{partial}{partial y}+vec{k}frac{partial}{partial z}$

物理含义:运动的流体微团的任一属性的时间变化率,$frac{partial}{partial t}$为当地导数,表示固定点处的时间变化率,$vec{V}cdotnabla$为迁移导数,表示由于流体微团从流场中一点到另一点,流场的空间不均匀性引起的时间变化率
- 速度散度:$nablacdotvec{V}$
$nablacdotvec{V}=frac{1}{delta upsilon} frac{D (delta upsilon)}{Dt}$
物理含义:每单位体积运动着的流体微团,体积随时间的变化率
1.3.2 连续性方程导出
1.3.2.1 空间位置固定的有限控制体模型
模型假设:形状任意、大小有限且位置固定的控制体
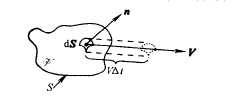
质量守恒假设:通过控制面S流出控制体的净质量流量=控制体内质量减少的时间变化率
通过控制面S流出控制体的净质量流量$=iint_S rho vec{V}dvec{S}$
控制体内质量减少的时间变化率$=frac{-partial{iiint_{mathscr v}rho d mathscr v}}{partial t}$
导出连续性方程:$frac{partial{iiint_{mathscr v}rho d mathscr v}}{partial t}+iint_S rho vec{V}dvec{S}=0$
1.3.2.2 随流体运动的有限控制体模型
模型假设:形状任意、大小有限且随流体流动的控制体
质量守恒假设:控制体质量不变
由物质导数的意义,可知该控制体质量的物质导数=0
导出连续性方程:$frac{D iiint_{mathscr v}rho d mathscr v}{Dt}=0$
1.3.2.3 空间位置固定的无穷小微团模型
模型假设:空间位置固定的无穷小微团
质量守恒假设:流出微团的净质量流量=微团质量减少的时间变化率
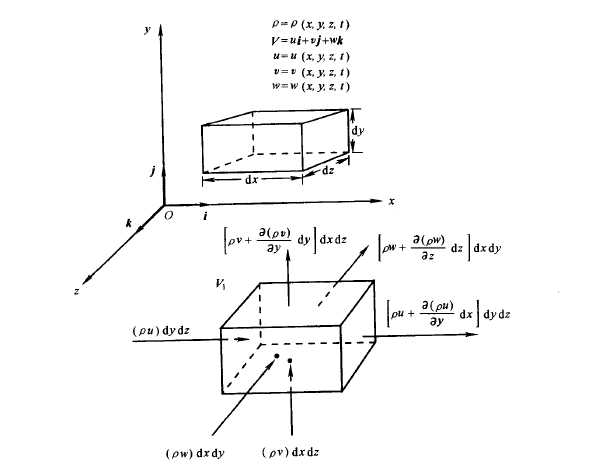
$x$方向流出的净质量流量:$[rho u+frac{partial(rho u)}{partial x}dx]dydz-(rho u)dydz=frac{partial(rho u)}{partial x}dxdydz$
$y$方向流出的净质量流量:$[rho v+frac{partial(rho v)}{partial y}dy]dxdz-(rho v)dxdz=frac{partial(rho v)}{partial y}dxdydz$
$z$方向流出的净质量流量:$[rho w+frac{partial(rho w)}{partial z}dz]dxdy-(rho w)dxdy=frac{partial(rho w)}{partial z}dxdydz$
流出微团的总净质量流量:$[frac{partial(rho u)}{partial x}+frac{partial(rho v)}{partial y}+frac{partial(rho w)}{partial z}]dxdydz$
微团质量减少的时间变化率:$-frac{partial rho}{partial t}dxdydz$
导出连续性方程:$[frac{partial(rho u)}{partial x}+frac{partial(rho v)}{partial y}+frac{partial(rho w)}{partial z}]dxdydz+frac{partial rho}{partial t}dxdydz=0$
化简为:$[frac{partial(rho u)}{partial x}+frac{partial(rho v)}{partial y}+frac{partial(rho w)}{partial z}]+frac{partial rho}{partial t}=0$
写成散度形式:$frac{partial rho}{partial t}+nabla(rho vec{V})=0$
1.3.2.4 随流体流动的无穷小微团模型
模型假设:随流体运动的微团,质量不变,但是形状和体积变化
质量守恒假设:微团质量不变
由物质导数的含义,该微团质量的物质导数=0,即$frac{D(delta m)}{Dt}=0$
又$delta m=rho delta mathscr{v}$
带入并整理得:$frac{Drho}{Dt}+rho[frac{1}{delta mathscr{v}} frac{D (delta mathscr{v})}{Dt}]=frac{Drho}{Dt}+rho nablacdotvec{V}=0$
注释
积分形式得方程允许固定的控制体内出现间断,因为积分的可积性允许被积函数出现间断,然而微分形式的方程要求控制体内必须是连续的,因为可微性要求函数必须是连续的。
1.3.3 动量方程导出
这里给出由运动的流体微团模型导出的动量方程。
模型假设:运动着的流体微团,质量不变,但是形状和体积变化
牛顿第二定律假设:作用于微团上力的总和等于其质量乘以当时的加速度
作用力的来源:
- 体积力:直接作用在整个微团上的力,作用是超距离的,如重力、电场力、磁场力等等
- 表面力:直接作用在微团表面的力,只能由两种原因引起:由包在微团周围的流体所施加的作用在微团表面的压力分布或是由于外部流体推拉微团,以摩擦的形式作用于表面的切应力和正应力分布(粘性力)
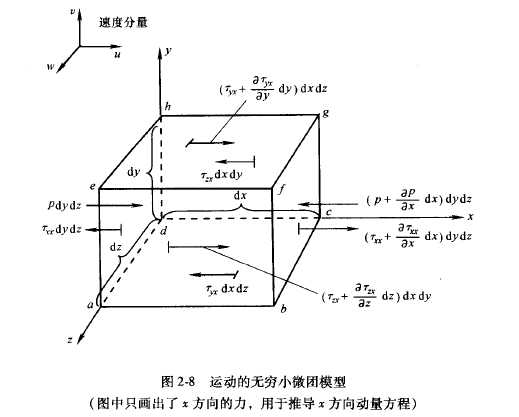
以作用在微团上$x$方向的力为例:
总体积力=$rho f_x(dxdydz)$
表面力:
压力:$pdydz$和$(p+frac{partial p}{partial x}dx)dydz$
正应力:$tau_{xx}dydz$和$(tau_{xx}+frac{partial tau_{xx}}{partial x}dx)dydz$
切应力:
$tau_{yx}dxdz$和$(tau_{yx}+frac{partial tau_{yx}}{partial y})dxdz$
$tau_{zx}dxdy$和$(tau_{zx}+frac{partial tau_{zx}}{partial z})dxdy$
$x$方向总的力:$F_x=(-frac{partial p}{partial x}+frac{partial tau_{xx}}{partial x}+frac{partial tau_{yx}}{partial y}+frac{partial tau_{zx}}{partial z})dxdydz+rho f_xdxdydz$
流动微团的质量:$m=rho dxdydz$
流动微团的加速度:$a_x=frac{Du}{Dt}$
导出$x$方向动量方程(粘性流):$(-frac{partial p}{partial x}+frac{partial tau_{xx}}{partial x}+frac{partial tau_{yx}}{partial y}+frac{partial tau_{zx}}{partial z})+rho f_x=rho frac{Du}{Dt}$
同样可分别得到$y$方向动量方程(粘性流):$(-frac{partial p}{partial y}+frac{partial tau_{xy}}{partial x}+frac{partial tau_{yy}}{partial y}+frac{partial tau_{zy}}{partial z})+rho f_y=rho frac{Dv}{Dt}$
$z$方向动量方程(粘性流):$(-frac{partial p}{partial z}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z})+rho f_z=rho frac{Dw}{Dt}$
以上称为Navier-Stokes方程的非守恒形式,它们都是标量形式
由它们可导出N-S方程的守恒形式:
因 $rho frac{Du}{Dt}=rho frac{partial u}{partial t}+rho (vec{V}cdot nabla)u$
$frac{partial (rho u)}{partial t}=rho frac{partial u}{partial t}+ufrac{partial rho}{partial t}$
$nablacdot(rho uvec{V})=unabla cdot(rho vec{V})+(rho vec{V})cdot nabla u $
$frac{partial rho}{partial t}+nabla(rho vec{V})=0$
带入整理得:
$rho frac{Du}{Dt}=frac {partial (rho u)}{partial t}+nablacdot(rho uvec{V})$
得到$x$方向N-S方程得守恒形式(粘性流):
$frac {partial (rho u)}{partial t}+nablacdot(rho uvec{V})=-frac{partial p}{partial x}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z}+rho f_x$
类似的,
$y$方向:$frac {partial (rho v)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial y}+frac{partial tau_{xy}}{partial x}+frac{partial tau_{yy}}{partial y}+frac{partial tau_{zy}}{partial z}+rho f_y$
$z$方向:$frac {partial (rho w)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial z}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z}+rho f_z$
1.3.4 能量方程导出
和上一节一样,还是基于运动的无穷小微团推导出能量方程
能量守恒定律假设:流体微团内能量的变化率=流入微团内的净热流量+体积力和表面力对微团做功的功率
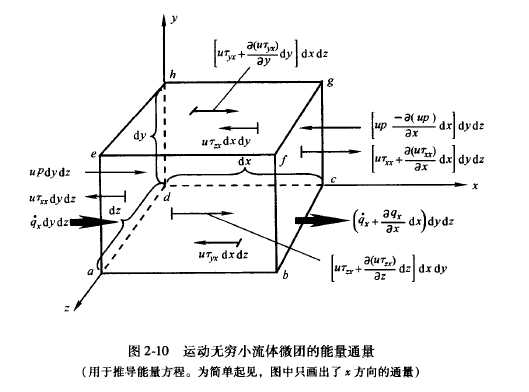
体积力做功的功率$=rho fcdot vec{V}dxdydz$
$x$方向上表面力做功的功率:
压力做功的功率:$[pudydz-(p+frac{partial (pu)}{partial x}dx)dydz]=-frac{partial (pu)}{partial x}dxdydz$
切应力做功的功率:
$[frac{partial utau_{xx}}{partial x}+frac{partial utau_{yx}}{partial y}+frac{partial utau_{zx}}{partial z}]dxdydz$
$x$方向所有表面力做功的功率:$[-frac{partial (pu)}{partial x}+frac{partial utau_{xx}}{partial x}+frac{partial utau_{yx}}{partial y}+frac{partial utau_{zx}}{partial z}]dxdydz$
所有方向总的做功功率:$-[(frac{partial (pu)}{partial x}+frac{partial (pv)}{partial y}+frac{partial (pw)}{partial z})+frac{partial utau_{xx}}{partial x}+frac{partial utau_{yx}}{partial y}+frac{partial utau_{zx}}{partial z}+frac{partial utau_{xy}}{partial x}+frac{partial utau_{yy}}{partial y}+frac{partial utau_{zy}}{partial z}+frac{partial utau_{xz}}{partial x}+frac{partial utau_{yz}}{partial y}+frac{partial utau_{zz}}{partial z}]dxdydz+rho fcdot vec{V}dxdydz$
流入微团的净热流量:
定义$dot q$为单位时间内通过垂直于某方向单位面积的能量(即该方向上的热流)
流体微团的体积加热率$=rho dot q dxdydz$
和正应力平行方向热传导对微团的加热$[dot q_x-(dot q_x+frac{partial dot q_x}{partial x}dx)]dydz=-frac{partial dot q_x}{partial x}dxdydz$
热传导对流体微团的总加热$-(frac{partial dot q_x}{partial x}+frac{partial dot q_y}{partial y}+frac{partial dot q_z}{partial z})dxdydz$
流入微团内的净热流量$[rho dot q-(frac{partial dot q_x}{partial x}+frac{partial dot q_y}{partial y}+frac{partial dot q_z}{partial z})]dxdydz$
根据傅里叶热传导定律,热传导产生的热流与当地的温度梯度成正比:
$dot q_x=-kfrac{partial T}{partial x}$ $dot q_y=-kfrac{partial T}{partial y}$ $dot q_z=-kfrac{partial T}{partial z}$
因此流入微团内的净热流量可改写为:$[rho dot q+frac{partial (kfrac{partial T}{partial x})}{partial x}+frac{partial (kfrac{partial T}{partial y})}{partial y}+frac{partial (kfrac{partial T}{partial z})}{partial z}]dxdydz$
微团的能量变化率:
运动流体微团的能量由两个来源:
- 由于分子随机运动而产生的内能,包括平动能、转动能、振动能和电子能
-
微团平动时的动能,单位质量动能为$V^2/2$
流体微团的能量变化率:$rhofrac{D(e+frac{V^2}{2})}{Dt}dxdydz$
导出能量方程(非守恒形式):
$begin{aligned} rho frac{mathrm{D}}{mathrm{D} t}left(e+frac{V^2}{2}right)= & rho dot{q}+frac{partial}{partial x}left(k frac{partial T}{partial x}right)+frac{partial}{partial y}left(k frac{partial T}{partial y}right)+frac{partial}{partial z}left(k frac{partial T}{partial z}right)- & frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+frac{partialleft(u tau_{x x}right)}{partial x}+frac{partialleft(u tau_{y x}right)}{partial y}+frac{partialleft(u tau_{z x}right)}{partial z}+ & frac{partialleft(v tau_{x y}right)}{partial x}+frac{partialleft(v tau_{y y}right)}{partial y}+frac{partialleft(v tau_{x y}right)}{partial z}+frac{partialleft(w tau_{x z}right)}{partial x}+frac{partialleft(w tau_{y z}right)}{partial y}+frac{partialleft(w tau_{z z}right)}{partial z}+rho f cdot Vend{aligned}$
对应的守恒形式能量方程:
$begin{aligned} & frac{partial}{partial t}left[rholeft(e+frac{V^2}{2}right)right]+nabla cdotleft[rholeft(e+frac{V^2}{2}right) boldsymbol{V}right] = & rho dot{q}+frac{partial}{partial x}left(k frac{partial T}{partial x}right)+frac{partial}{partial y}left(k frac{partial T}{partial y}right)+frac{partial}{partial z}left(k frac{partial T}{partial z}right)-frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+ & frac{partialleft(u tau_{x z}right)}{partial x}+frac{partialleft(u tau_{y z}right)}{partial y}+frac{partialleft(u tau_{z x}right)}{partial z}+frac{partialleft(v tau_{x y}right)}{partial x}+frac{partialleft(v tau_{y z}right)}{partial y}+frac{partialleft(u tau_{z y}right)}{partial z}+ & frac{partialleft(w tau_{x z}right)}{partial x}+frac{partialleft(w tau_{y z}right)}{partial y}+frac{partialleft(w tau_zright)}{partial z}+rho f cdot boldsymbol{V}end{aligned}$
1.3.5 总结
1.3.5.1 粘性流动的N-S方程(非定常三维可压缩粘性流动控制方程)
- 连续性方程
非守恒形式:$frac{Drho}{Dt}+rho nablacdotvec{V}$=0
守恒形式:$frac{partial rho}{partial t}+nabla(rho vec{V})=0$
- 动量方程
非守恒形式:
$x$方向 $rho frac{Du}{Dt}=(-frac{partial p}{partial x}+frac{partial tau_{xx}}{partial x}+frac{partial tau_{yx}}{partial y}+frac{partial tau_{zx}}{partial z})+rho f_x$
$y$方向 $rho frac{Dv}{Dt}=(-frac{partial p}{partial y}+frac{partial tau_{xy}}{partial x}+frac{partial tau_{yy}}{partial y}+frac{partial tau_{zy}}{partial z})+rho f_y$
$z$方向 $rho frac{Dw}{Dt}=(-frac{partial p}{partial z}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z})+rho f_z$
守恒形式:
$x$方向 $frac {partial (rho u)}{partial t}+nablacdot(rho uvec{V})=-frac{partial p}{partial x}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z}+rho f_x$
$y$方向 $frac {partial (rho v)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial y}+frac{partial tau_{xy}}{partial x}+frac{partial tau_{yy}}{partial y}+frac{partial tau_{zy}}{partial z}+rho f_y$
$z$方向 $frac {partial (rho w)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial z}+frac{partial tau_{xz}}{partial x}+frac{partial tau_{yz}}{partial y}+frac{partial tau_{zz}}{partial z}+rho f_z$
- 能量方程
非守恒形式:
$begin{aligned} rho frac{mathrm{D}}{mathrm{D} t}left(e+frac{V^2}{2}right)= & rho dot{q}+frac{partial}{partial x}left(k frac{partial T}{partial x}right)+frac{partial}{partial y}left(k frac{partial T}{partial y}right)+frac{partial}{partial z}left(k frac{partial T}{partial z}right)- & frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+frac{partialleft(u tau_{x x}right)}{partial x}+frac{partialleft(u tau_{y x}right)}{partial y}+frac{partialleft(u tau_{z x}right)}{partial z}+ & frac{partialleft(v tau_{x y}right)}{partial x}+frac{partialleft(v tau_{y y}right)}{partial y}+frac{partialleft(v tau_{x y}right)}{partial z}+frac{partialleft(w tau_{x z}right)}{partial x}+frac{partialleft(w tau_{y z}right)}{partial y}+frac{partialleft(w tau_{z z}right)}{partial z}+rho f cdot Vend{aligned}$
守恒形式:
$begin{aligned} & frac{partial}{partial t}left[rholeft(e+frac{V^2}{2}right)right]+nabla cdotleft[rholeft(e+frac{V^2}{2}right) boldsymbol{V}right] = & rho dot{q}+frac{partial}{partial x}left(k frac{partial T}{partial x}right)+frac{partial}{partial y}left(k frac{partial T}{partial y}right)+frac{partial}{partial z}left(k frac{partial T}{partial z}right)-frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+ & frac{partialleft(u tau_{x z}right)}{partial x}+frac{partialleft(u tau_{y z}right)}{partial y}+frac{partialleft(u tau_{z x}right)}{partial z}+frac{partialleft(v tau_{x y}right)}{partial x}+frac{partialleft(v tau_{y z}right)}{partial y}+frac{partialleft(u tau_{z y}right)}{partial z}+ & frac{partialleft(w tau_{x z}right)}{partial x}+frac{partialleft(w tau_{y z}right)}{partial y}+frac{partialleft(w tau_zright)}{partial z}+rho f cdot boldsymbol{V}end{aligned}$
1.3.5.2 无粘流欧拉方程(非定常三维可压缩无粘流控制方程)
无粘流的定义是忽略了耗散、粘性输运、质量扩散以及热传导的流动,因此只要将上一节中所有包含摩擦和热传导的项去掉即可的到无粘流方程
- 连续性方程
非守恒形式:$frac{Drho}{Dt}+rho nablacdotvec{V}$=0
守恒形式:$frac{partial rho}{partial t}+nabla(rho vec{V})=0$
- 动量方程
非守恒形式:
$x$方向 $rho frac{Du}{Dt}=-frac{partial p}{partial x}+rho f_x$
$y$方向 $rho frac{Dv}{Dt}=-frac{partial p}{partial y}+rho f_y$
$z$方向 $rho frac{Dw}{Dt}=-frac{partial p}{partial z}+rho f_z$
守恒形式:
$x$方向 $frac {partial (rho u)}{partial t}+nablacdot(rho uvec{V})=-frac{partial p}{partial x}+rho f_x$
$y$方向 $frac {partial (rho v)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial y}+rho f_y$
$z$方向 $frac {partial (rho w)}{partial t}+nablacdot(rho vvec{V})=-frac{partial p}{partial z}+rho f_z$
- 能量方程
非守恒形式:
$begin{aligned} rho frac{mathrm{D}}{mathrm{D} t}left(e+frac{V^2}{2}right)= & rho dot{q}- frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+rho f cdot Vend{aligned}$
守恒形式:
$begin{aligned} & frac{partial}{partial t}left[rholeft(e+frac{V^2}{2}right)right]+nabla cdotleft[rholeft(e+frac{V^2}{2}right) boldsymbol{V}right] = & rho dot{q}- frac{partial(u p)}{partial x}-frac{partial(v p)}{partial y}-frac{partial(w p)}{partial z}+rho f cdot Vend{aligned}$
2. 有限差分法(待完善)
CFD的方法介绍:微分方程数值求解——有限差分法 - 知乎 (zhihu.com)
3. 12 Steps to Navier-Stokes(补充代码)
Step 1: 1-D Linear Convection
首先来看1维线性对流方程:
$begin{cases}
& frac{partial u}{partial t} +cfrac{partial u}{partial x} =0
& u(x,0)=u|_0 (x)
end{cases}
$
该方程的含义是:当给定初始条件的时,初始波以速度$c$移动,同时移动过程中不改变其形状。由给出的初始条件,可以求出该方程的精确解:
$u(x,t)=u_{0} (x-ct)$
将上面的方程在时间和空间上离散化,对时间导数向前差分,空间导数向后差分,时间间隔为$ Delta t$,空间坐标系下$x$轴划分为N+1个点,记为$i$从0到N。
我们知道导数可以近似这样表示:
$frac{partial u}{partial t} approx frac{u(x+Delta x)-u(x)}{Delta x} $
方程离散化之后变为:
$frac{u_{i}^{n+1}-u_{i}^{n} }{Delta t} +cfrac{u_{i}^{n}-u_{i-1}^{n} }{Delta x}=0$
$n$和$n+1$是时间上两个连续的步骤,$i-1$到$i$是离散化$x$轴上两个相邻点。如果给定了初始条件,那么我们只需要求出$u_{i}^{n+1}$,而我们可以用其他离散点来表示$u_{i}^{n+1}$:
$u_{i}^{n+1}=u_{i}^{n}-cfrac{Delta t}{Delta x}(u_{i}^{n}-u_{i-1}^{n})$
Step 2: 1-D Nolinear Convection
1维非线性对流方程:
$begin{cases}
& frac{partial u}{partial t} +ufrac{partial u}{partial x} =0
& u(x,0)=u_{0} (x)
end{cases}
$
同样是对方程离散化:
$frac{u_{i}^{n+1}-u_{i}^{n} }{Delta t} +{u_{i}^{n}}frac{u_{i}^{n}-u_{i-1}^{n} }{Delta x}=0$
同样,我们只需要求解$u_{i}^{n+1}$:
$u_{i}^{n+1}=u_{i}^{n}-{u_{i}^{n}}frac{Delta t}{Delta x}(u_{i}^{n}-u_{i-1}^{n})$
数值耗散和数值色散
在进行第一第二步过程中,调整离散化程度(网格数)会极大改变最后求出的波函数u。
原因在于对于线性PDE,对于其精确解我们常常使用线性傅里叶分析方法,而我们采用差分分析方法来求其数值解,两种方式的差异导致解之间存在耗散与色散,借用波的特性,耗散对应振幅,色散对应相位。当我们采用不同的差分方式,比如向前差分、向后差分、中心差分等,会产生不同的耗散,影响到差分离散格式的稳定性,往往我们需要在计算时添加人工粘性。而数值解由于存在色散,不同波数成分相速度不同,经过一定时间后,各个波数成分的叠加不会完全恢复精确解的波形,从而造成波形畸变。
我们可以通过定义数值耗散和数值色散的分辨率,从而来表征数值格式解对于复杂问题的分辨率。
以我们研究的一维对流方程为例,由于在每个$Delta t$时间范围内,我们假定波传播的距离为$dx$,但是实际波传播的距离大于$dx$,这导致产生了相位差(色散),随着$Delta t$的不断累积,相位差不断扩大,导致数值解和精确解的差距越来越大(波形畸变)。
我们可以利用CFL数来计算合理的$dt$,而$dt$又由$dx$和$u$决定。
$sigma =frac{u Delta t}{Delta x} le sigma_{max} $
u: 波速
$sigma$: 库朗数
$sigma_{max} $:用于确保离散格式的稳定性
(待完善)
Step 3: Diffusion Equation in 1-D
来看1维扩散方程:
$frac{partial u}{partial t} =v frac{{partial}^2 u}{{partial}^2 x} $
使用中心差分格式对$frac{{partial}^2 u}{{partial}^2 x}$离散化,而我们知道$u_i$附近的$u_{i+1}$和$u_{i-1}$的泰勒展开(差分近似)为:
$begin{aligned} & u_{i+1}=u_i+left.Delta x frac{partial u}{partial x}right|i+left.frac{Delta x^2}{2} frac{partial^2 u}{partial x^2}right|i+left.frac{Delta x^3}{3 !} frac{partial^3 u}{partial x^3}right|_i+Oleft(Delta x^4right) & u{i-1}=u_i-left.Delta x frac{partial u}{partial x}right|i+left.frac{Delta x^2}{2} frac{partial^2 u}{partial x^2}right|_i-left.frac{Delta x^3}{3 !} frac{partial^3 u}
{partial x^3}right|_i+Oleft(Delta x^4right)end{aligned}$
可以看出,两者泰勒展开的导数奇数阶加和后相互抵消,因此只剩下零阶和二阶导项。
$begin{aligned} & u{i+1}+u_i=2u_i+left.{Delta x^2} frac{partial^2 u}{partial x^2}right|i+Oleft(Delta x^4right) end{aligned}$
所以二阶导项$left.frac{partial^2 u}{partial x^2} right|_i$表示为:
$left.frac{partial^2 u}{partial x^2} right|_i=frac{u{i+1}-2u_i+u{i-1}}{Delta x^2}+O(Delta x^2)$
将上述差分格式带入到1维扩散方程中:
$frac{u_{i+1}-u_i}{Delta t}=nu frac{u_{i+1}-2u_i+u_{i-1}}{Delta x^2}$,当我们知道了初始条件,$u_{i}^{n+1}$就可以求出来,将上式整理为:
$u_{i}^{n+1}=u_{i}^{n}+frac{nu Delta t}{Delta x^2}(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n})$
Step 4: Burger's Equation
1-D方向的Burger's方程:
$frac{partial u}{partial t} +ufrac{partial u}{partial x}=v frac{{partial}^2 u}{{partial}^2 x} $
左半部分为一维非线性对流方程的左半边,右半部分为一维扩散方程的右半边。
同样,我们对该方程离散化:
$frac{u_{i}^{n+1}-u_{i}^{n} }{Delta t} +{u_{i}^{n}}frac{u_{i}^{n}-u_{i-1}^{n} }{Delta x}=vfrac{u_{i+1}-2u_i+u_{i-1}}{Delta x^2}$
$u_{i}^{n+1}$可表示为:
$u_{i}^{n+1}=u_{i}^{n}-u_{i}^{n}frac{Delta t}{Delta x}(u_{i}^{n}-u_{i-1}^{n})+vfrac{Delta t}{Delta x^2}(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n})$
Burger's方程的初始条件和边界条件:
- 初始条件
$u = frac{2nu}{phi}frac{partialphi}{partial x}+4$
$phi = exp(frac{-x^2}{4nu})+exp(frac{-(x-2pi)^2}{4nu})$
它们的解析解分别为:
$u = frac{2nu}{phi}frac{partialphi}{partial x}+4$
$phi = exp(frac{-(x-4pi)^2}{4nu(t+1)})+exp(frac{-(x--4t-2pi)^2}{4nu(t+1)})$
- 边界条件
$u(0) = u(2pi)$为周期性边界条件
Step 5: 2-D Linear Convection
2D 线性对流的PDE:
$frac{partial u}{partial t} +cfrac{partial u}{partial x} +cfrac{partial u}{partial y}=0$
离散化为:
$frac{u_{i,j}^{n+1}-u_{i,j}^{n} }{Delta t} +cfrac{u_{i,j}^{n}-u_{i-1,j}^{n} }{Delta x}+cfrac{u_{i,j}^{n}-u_{i,j-1}^{n} }{Delta x}=0$
$u_{i,j}^{n+1}$表示为:
$u_{i,j}^{n+1}=u_{i,j}^{n}-cfrac{Delta t}{Delta x}(u_{i,j}^{n}-u_{i-1,j}^{n})-cfrac{Delta t}{Delta y}(u_{i,j}^{n}-u_{i,j-1}^{n})$
Step 6: 2-D Convection
2D 对流PDE:
$frac{partial u}{partial t} +ufrac{partial u}{partial x} +vfrac{partial u}{partial y}=0$
$frac{partial v}{partial t} +ufrac{partial v}{partial x} +vfrac{partial v}{partial y}=0$
分别进行离散化:
$frac{u_{i,j}^{n+1}-u_{i,j}^{n} }{Delta t} +u_{i,j}^{n}frac{u_{i,j}^{n}-u_{i-1,j}^{n} }{Delta x}+v_{i,j}^{n}frac{u_{i,j}^{n}-u_{i,j-1}^{n} }{Delta x}=0$
$frac{v_{i,j}^{n+1}-v_{i,j}^{n} }{Delta t} +v_{i,j}^{n}frac{v_{i,j}^{n}-v_{i-1,j}^{n} }{Delta x}+v_{i,j}^{n}frac{v_{i,j}^{n}-v_{i,j-1}^{n} }{Delta x}=0$
那么$u_{i,j}^{n+1}$和$v_{i,j}^{n+1}$可表示为:
$u_{i,j}^{n+1}=u_{i,j}^{n}-u_{i,j}^nfrac{Delta t}{Delta x}(u_{i,j}^{n}-u_{i-1,j}^{n})-v_{i,j}^nfrac{Delta t}{Delta y}(u_{i,j}^{n}-u_{i,j-1}^{n})$
$v_{i,j}^{n+1}=v_{i,j}^{n}-u_{i,j}^nfrac{Delta t}{Delta x}(v_{i,j}^{n}-v_{i-1,j}^{n})-v_{i,j}^nfrac{Delta t}{Delta y}(v_{i,j}^{n}-v_{i,j-1}^{n})$
Step 7: 2-D Diffusion
2D 扩散方程:
$frac{partial u}{partial t} =v frac{{partial}^2 u}{{partial}^2 x}+v frac{{partial}^2 u}{{partial}^2 y} $
离散化:
$frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{Delta t}=nu frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{Delta x^2}+nu frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{Delta y^2}$
整理为:
$
u_{i,j}^{n+1}=u_{i,j}^{n}+frac{nu Delta t}{Delta x^2}(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n})+frac{nu Delta t}{Delta x^2}(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n})
$
Step 8: 2-D Burger's Equation
2D Burger's 方程
$frac{partial u}{partial t} +ufrac{partial u}{partial x}+vfrac{partial u}{partial y}=v (frac{{partial}^2 u}{{partial}^2 x}+frac{{partial}^2 u}{{partial}^2 y})$
$frac{partial v}{partial t} +ufrac{partial v}{partial x}+vfrac{partial v}{partial y}=v (frac{{partial}^2 v}{{partial}^2 x}+frac{{partial}^2 v}{{partial}^2 y})$
离散化:
$begin{aligned} & frac{u_{i, j}^{n+1}-u_{i, j}^n}{Delta t}+u_{i, j}^n frac{u_{i, j}^n-u_{i-1, j}^n}{Delta x}+v_{i, j}^n frac{u_{i, j}^n-u_{i, j-1}^n}{Delta y}= & nuleft(frac{u_{i+1, j}^n-2 u_{i, j}^n+u_{i-1, j}^n}{Delta x^2}+frac{u_{i, j+1}^n-2 u_{i, j}^n+u_{i, j-1}^n}{Delta y^2}right) & frac{v_{i, j}^{n+1}-v_{i, j}^n}{Delta t}+u_{i, j}^n frac{v_{i, j}^n-v_{i-1, j}^n}{Delta x}+v_{i, j}^n frac{v_{i, j}^n-v_{i, j-1}^n}{Delta y}= & nuleft(frac{v_{i+1, j}^n-2 v_{i, j}^n+v_{i-1, j}^n}{Delta x^2}+frac{v_{i, j+1}^n-2 v_{i, j}^n+v_{i, j-1}^n}{Delta y^2}right) & end{aligned}$
化简为:
$begin{aligned} u_{i, j}^{n+1}= & u_{i, j}^n-frac{Delta t}{Delta x} u_{i, j}^nleft(u_{i, j}^n-u_{i-1, j}^nright)-frac{Delta t}{Delta y} v_{i, j}^nleft(u_{i, j}^n-u_{i, j-1}^nright) & +frac{nu Delta t}{Delta x^2}left(u_{i+1, j}^n-2 u_{i, j}^n+u_{i-1, j}^nright)+frac{nu Delta t}{Delta y^2}left(u_{i, j+1}^n-2 u_{i, j}^n+u_{i, j-1}^nright) v_{i, j}^{n+1}= & v_{i, j}^n-frac{Delta t}{Delta x} u_{i, j}^nleft(v_{i, j}^n-v_{i-1, j}^nright)-frac{Delta t}{Delta y} v_{i, j}^nleft(v_{i, j}^n-v_{i, j-1}^nright) & +frac{nu Delta t}{Delta x^2}left(v_{i+1, j}^n-2 v_{i, j}^n+v_{i-1, j}^nright)+frac{nu Delta t}{Delta y^2}left(v_{i, j+1}^n-2 v_{i, j}^n+v_{i, j-1}^nright)end{aligned}$
Step 9: 2-D Laplace Equation
2D Laplace PDE:
$frac{{partial}^2 p}{{partial}^2 x}+frac{{partial}^2 p}{{partial}^2 y}=0$
Laplace 方程的二阶导项需要用中心差分来离散化:
$frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{Delta x^2}+frac{p_{i,j+1}^{n}-2p_{i,j}^{n}+p_{i,j-1}^{n}}{Delta y^2}=0$
Laplace 方程没有时间变量,因此没有n+1,其研究的是系统的均衡态。上式整理后得:
$begin{aligned} p_{i, j}^{n}= frac{Delta y^2(p_{i+1, j}^{n}+p_{i-1, j}^{n})+Delta x^2(p_{i, j+1}^{n}+p_{i, j-1}^{n})}{2(Delta x^2+Delta y^2)} end{aligned}$
Step 10: 2-D Poisson Equation
对于不可压缩流体的N-S方程如下:
$nabla cdot vec{v}=0$
$frac{partial vec{v} }{partial t} +(vec{v}cdot nabla )vec{v}=-frac{1}{rho}nabla p +nu nabla ^{2}vec{v} $
上面的方程为连续性方程,代表了质量守恒,此时密度不变。下面的方程代表了动量守恒。对于上面的不可压缩流体的连续性方程,由于没有其他变量,无法建立其速度和压力之间的关系,但是在可压缩流体中不是如此。
不过由于$nabla cdot vec{v}=0$提供了流体运动约束,压力场需要变化,以确保$nabla cdot vec{v}$处处为零。我们可以通过泊松方程来使压力场满足这样的条件。
泊松方程就是非线性的Laplace方程
$frac{{partial}^2 p}{{partial}^2 x}+frac{{partial}^2 p}{{partial}^2 y}=b$
和上一节的处理方式一样,离散化得到:
$frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{Delta x^2}+frac{p_{i,j+1}^{n}-2p_{i,j}^{n}+p_{i,j-1}^{n}}{Delta y^2}=b_{i,j}^n$
化简得到:
$begin{aligned} p_{i, j}^{n}= frac{Delta y^2(p_{i+1, j}^{n}+p_{i-1, j}^{n})+Delta x^2(p_{i, j+1}^{n}+p_{i, j-1}^{n})-b_{i,j}^nDelta x^2Delta y^2}{2(Delta x^2+Delta y^2)} end{aligned}$
为了求解此方程,假定
初始时刻$p=0$
边界条件$p=0 at x=0,2 and y=0,1$
$b_{i,j}$:
$b_{i,j}=100 at i=frac{1}{4}nx,j=frac{1}{4}ny$
$b_{i,j}=-100 at i=frac{3}{4}nx,j=frac{3}{4}ny$
$b_{i,j}=0 everywhere else$
Step 11: Cavity Flow with Navier-Stokes
由上一节,我们知道对于不可压缩流体的速度分量$ vec{v} $的动量方程为:
$frac{partial vec{v} }{partial t} +(vec{v}cdot nabla )vec{v}=-frac{1}{rho}nabla p +nu nabla ^{2}vec{v} $
类似的我们可以写出其他速度分量下的动量方程。
此处我们研究的是二维的情况,因此有两个速度分量,对应的动量方程为:
算子形式:
$frac{partial vec{v} }{partial t} +(vec{v}cdot nabla )vec{v}=-frac{1}{rho}nabla p +nu nabla ^{2}vec{v} $
$frac{partial vec{u} }{partial t} +(vec{u}cdot nabla )vec{u}=-frac{1}{rho}nabla p +nu nabla ^{2}vec{u} $
笛卡尔坐标系下形式:
$frac{partial v }{partial t} +ufrac{partial v }{partial x}+vfrac{partial v }{partial y}=-frac{1}{rho}frac{partial p }{partial y} +nu( frac{{partial}^2 v}{{partial}^2 x}+frac{{partial}^2 v}{{partial}^2 y})$
$frac{partial u }{partial t} +ufrac{partial u }{partial x}+vfrac{partial u }{partial y}=-frac{1}{rho}frac{partial p }{partial x} +nu( frac{{partial}^2 u}{{partial}^2 x}+frac{{partial}^2 u}{{partial}^2 y})$
再加上二维情况下的压力方程:
$frac{{partial}^2 p}{{partial}^2 x}+frac{{partial}^2 p}{{partial}^2 y}=-rho(frac{partial u }{partial x}frac{partial u }{partial x}+2frac{partial u }{partial y}frac{partial v }{partial x}+frac{partial v }{partial y}frac{partial v }{partial y})$
对上述方程离散化,可得到求解速度和压力的方式:
$$
begin{aligned}
u_{i, j}^{n+1}=u_{i, j}^n & -u_{i, j}^n frac{Delta t}{Delta x}left(u_{i, j}^n-u_{i-1, j}^nright)-v_{i, j}^n frac{Delta t}{Delta y}left(u_{i, j}^n-u_{i, j-1}^nright)
& -frac{Delta t}{rho 2 Delta x}left(p_{i+1, j}^n-p_{i-1, j}^nright)
& +nuleft(frac{Delta t}{Delta x^2}left(u_{i+1, j}^n-2 u_{i, j}^n+u_{i-1, j}^nright)+frac{Delta t}{Delta y^2}left(u_{i, j+1}^n-2 u_{i, j}^n+u_{i, j-1}^nright)right)
end{aligned}
$$
$$
begin{aligned}
v_{i, j}^{n+1}=v_{i, j}^n & left.-u_{i, j}^n frac{Delta t}{Delta x}left(v_{i, j}^n-v_{i-1, j}^nright)-v_{i, j}^n frac{Delta t}{Delta y}left(v_{i, j}^n-v_{i, j-1}^nright)right)
& -frac{Delta t}{rho 2 Delta y}left(p_{i, j+1}^n-p_{i, j-1}^nright)
& +nuleft(frac{Delta t}{Delta x^2}left(v_{i+1, j}^n-2 v_{i, j}^n+v_{i-1, j}^nright)+frac{Delta t}{Delta y^2}left(v_{i, j+1}^n-2 v_{i, j}^n+v_{i, j-1}^nright)right)
end{aligned}
$$
$$
begin{aligned}
p_{i, j}^n= & frac{left(p_{i+1, j}^n+p_{i-1, j}^nright) Delta y^2+left(p_{i, j+1}^n+p_{i, j-1}^nright) Delta x^2}{2left(Delta x^2+Delta y^2right)}
& -frac{rho Delta x^2 Delta y^2}{2left(Delta x^2+Delta y^2right)}
& timesleft[frac{1}{Delta t}left(frac{u_{i+1, j}-u_{i-1, j}}{2 Delta x}+frac{v_{i, j+1}-v_{i, j-1}}{2 Delta y}right)-frac{u_{i+1, j}-u_{i-1, j}}{2 Delta x} frac{u_{i+1, j}-u_{i-1, j}}{2 Delta x}right.
& left.-2 frac{u_{i, j+1}-u_{i, j-1}}{2 Delta y} frac{v_{i+1, j}-v_{i-1, j}}{2 Delta x}-frac{v_{i, j+1}-v_{i, j-1}}{2 Delta y} frac{v_{i, j+1}-v_{i, j-1}}{2 Delta y}right]
end{aligned}
$$
设定边界条件:
$u=1$ at $y=2$;
$u,v=0$ on the other boundaries;
$frac{partial p }{partial y}=0$ at $y=0$
$p=0$ at $y=2$
$frac{partial p }{partial x}=0$ at $x=0,2$

Comments NOTHING