截面被定义为与纤维束路径切线垂直的平面截断纤维束时,纤维束在该平面上形成的二维形状。由于纤维束被视为实体体积,截面被近似为包围纤维束内所有纤维的最小区域(通常是凸形)。截面的轮廓可以使用二维参数方程来定义。已经探索了各种形状,包括Peirce提出的椭圆、幂椭圆和Hearle和Shanahan提出的改进的透镜形状。
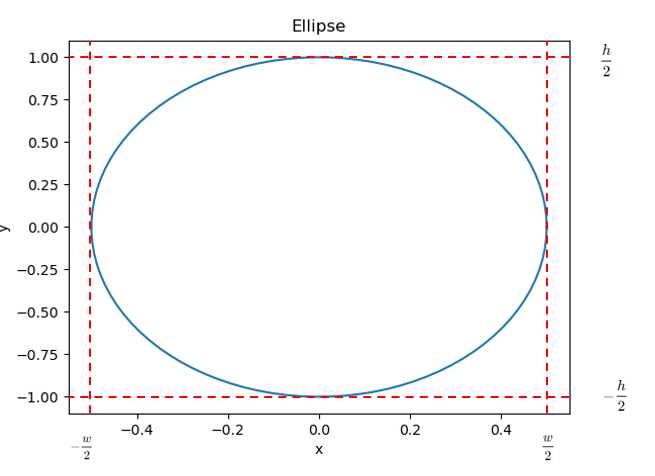
1.椭圆
$$
\begin{aligned}C(v)_x&=\frac{w}{2}\mathrm{cos}(2\pi v)&&0\leq v\leq1\\C(v)_y&=\frac{h}{2}\mathrm{sin}(2\pi v)&&0\leq v\leq1\end{aligned}
$$
import numpy as np
import matplotlib.pyplot as plt
import math
"""Ellipse"""
def C_xy(v, w, h):
x = w/2 * math.cos(2*np.pi*v)
y = h/2 * math.sin(2*np.pi*v)
return x, y
w = 1 #the width of the yarn cross section
h = 2 #the height of the yarn cross section
v = np.arange(0, 1.01, 0.01)
x = []
y = []
for i in v:
x_1, y_1 = C_xy(i, w, h)
x.append(x_1)
y.append(y_1)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Ellipse')
plt.show()
2.幂椭圆
$$
\begin{array}{rcl}\mathbf{C}(v)_x&=&\dfrac{w}{2}\cos(2\pi v)\quad0\leq t\leq1\\{C}(v)_y&=&\begin{cases}&\dfrac{h}{2}(\sin(2\pi v))^n&\text{if }0\leq t\leq0.5\\&-\dfrac{h}{2}(-\sin(2\pi v))^n&\text{if }0.5\leq t\leq1\end{cases}\end{array}
$$
在这里引用的是"Geometric and Mechanical Modelling of Textiles"文献中的相关公式。
import numpy as np
import matplotlib.pyplot as plt
import math
"""Power ellipse"""
def C_xy(v, w,h, n):
x = w / 2 * math.cos(2 * np.pi * v)
y =0
if v >= 0 and v <= 0.5:
y = (h/2) * math.sin(2*np.pi*v)**n
elif v >= 0.5 and v <= 1:
y = -(h/2)*(-math.sin(2*np.pi*v))**n
return x,y
# 定义参数
w = 1 #the width of the yarn cross section
h = 2 #the height of the yarn cross section
n = 2# power index
v = np.arange(0, 1.01, 0.01)
x = []
y = []
for i in v:
x_1, y_1 = C_xy(i, w, h,n)
x.append(x_1)
y.append(y_1)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Power ellipse')
plt.show()
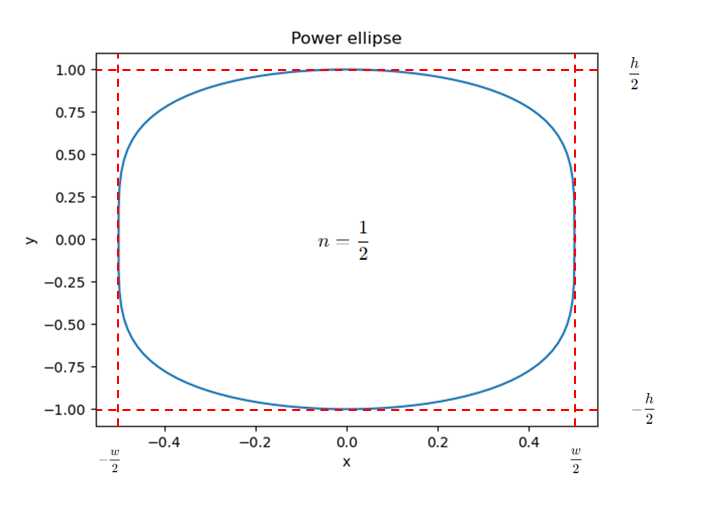
幂指数n=1/2时,图像为
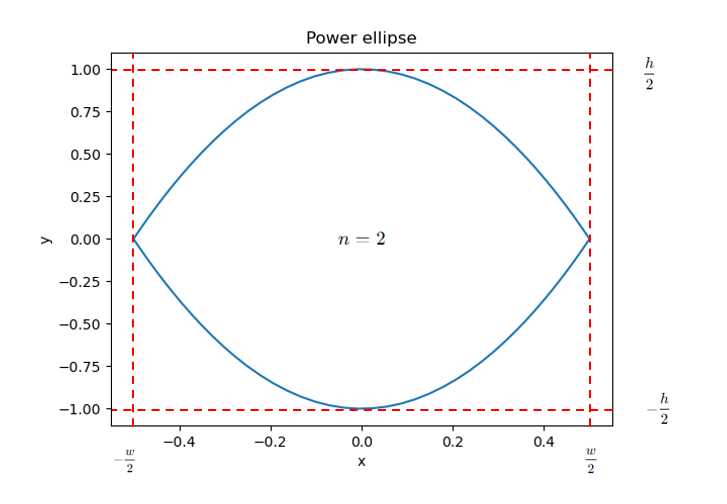
幂指数n=2时,图像为
3.透镜形状
透镜状横截面被定义为由半径为r1和r2的两个圆相交形成,它们分别垂直偏移距离o1和o2。参数r1、r2、o1和o2可以从所需的透镜截面的宽度w、高度h和畸变d计算得出:
"Automated geometric modelling of textile structures"
$$
\begin{aligned}r_1&=\frac{w^2+(h-2d)^2}{4(h-2d)},\quad r_2=\frac{w^2+(h+2d)^2}{4(h+2d)}\\o_1&=-r_1+\frac{h}{2}\quad o_2=r_1-\frac{h}{2}\end{aligned}
$$
$$
C(v)_x=\begin{cases}r_1\cos\theta+o_1&0\leq v\leq0.5\\-r_2\cos\theta+o_2&0.5\leq v\leq1\\\end{cases}\\C(v)_y=\begin{cases}r_1\cos\theta+o_1&0\leq v\leq0.5\\-r_2\cos\theta+o_2&0.5\leq v\leq1\end{cases}
$$
$$
\theta=\begin{cases}(1-4v)\sin^{-1}\left(\frac{w}{2r_1}\right)&0\leq v\leq0.5\\(-3+4v)\sin^{-1}\left(\frac{w}{2r_2}\right)_2&0.5\leq v\leq1\end{cases}
$$
公式中$C(v)_x$和$C(v)_y$相等,图像为直线。
"Geometric and Mechanical Modelling of Textiles"
$$
\begin{aligned}r_1&=\frac{w^2+(h-2d)^2}{4(h-2d)},\quad r_2=\frac{w^2+(h+2d)^2}{4(h+2d)}\\o_1&=-r_1+\frac{h}{2}\quad o_2=r_2-\frac{h}{2}\end{aligned}
$$
$$
C(v)_x=\begin{cases}r_1\sin\theta&0\leq v\leq0.5\\r_2\sin\theta&0.5\leq v\leq1\\\end{cases}\\C(v)_y=\begin{cases}r_1\cos\theta+o_1&0\leq v\leq0.5\\-r_2\cos\theta+o_2&0.5\leq v\leq1\end{cases}
$$
$$
\theta=\begin{cases}(1-4v)\sin^{-1}\left(\frac{w}{2r_1}\right)&0\leq v\leq0.5\\(-3+4v)\sin^{-1}\left(\frac{w}{2r_2}\right)&0.5\leq v\leq1\end{cases}
$$
import math
import matplotlib.pyplot as plt
import numpy as np
"""Lenticular
The lenticular cross-section is the intersection of two circles of radii r1 and r2 each offset
vertically by distances o1 and o2 respectively. """
def C_xy(v, w, r1, r2, o1, o2):
x = 0
y = 0
# 判断 (w / (2 * r1)) 和 (w / (2 * r2)) 的值是否在 -1 到 1 范围内
if not (-1 <= (w / (2 * r1)) <= 1) or not (-1 <= (w / (2 * r2)) <= 1):
return x, y
if v >= 0 and v <= 0.5:
theta = (1 - 4 * v) * math.asin(w / (2 * r1))
x = r1 * math.sin(theta)
y = r1 * math.cos(theta) + o1
elif v >= 0.5 and v <= 1:
theta = (-3 + 4 * v) * math.asin(w / (2 * r2))
x = r2 * math.sin(theta)
y = -r2 * math.cos(theta) + o2
return x, y
# 参数
w = 3 #the width of the yarn cross section
h = 2 #the height of the yarn cross section
d = 0.5 #distortion distance
r1 = (w ** 2 + (h - 2 * d) ** 2) / (4 * (h - 2 * d))
r2 = (w ** 2 + (h + 2 * d) ** 2) / (4 * (h + 2 * d))
o1 = -r1 + h / 2
o2 = r2 - h / 2
v = np.arange(0, 1.01, 0.01)
x = []
y = []
for i in v:
x_1, y_1 = C_xy(i, w, r1, r2, o1, o2)
x.append(x_1)
y.append(y_1)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Lenticular')
plt.show()
当w=1,d=0.5时,绘制出来的图像
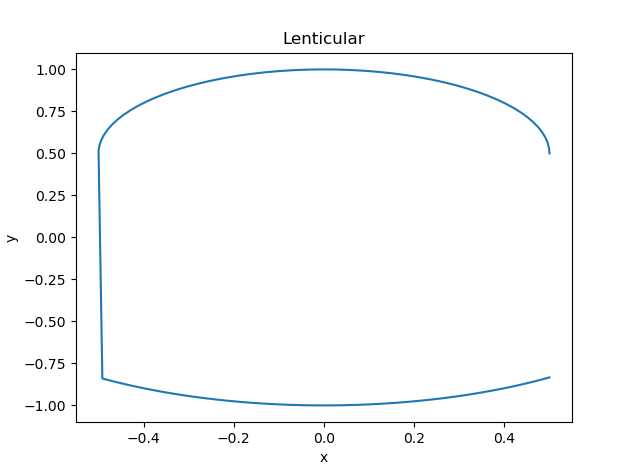
如果将w=10,d=0.5时,绘制出来的图像与标准图像相同 (当w从3开始,绘制出来的图像都与标准图像相同)
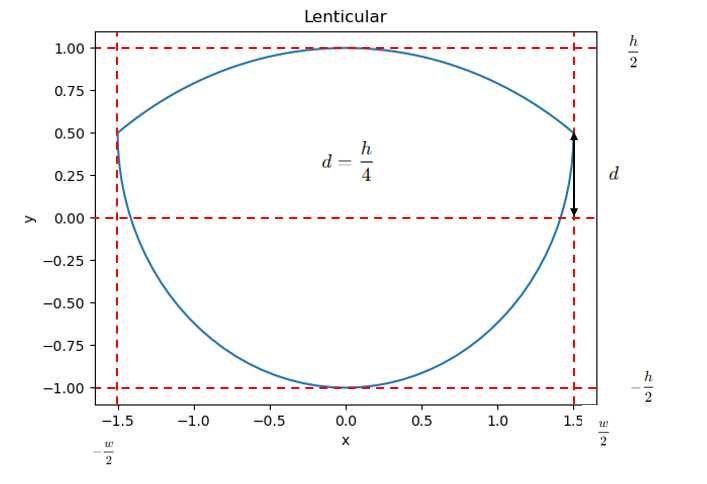
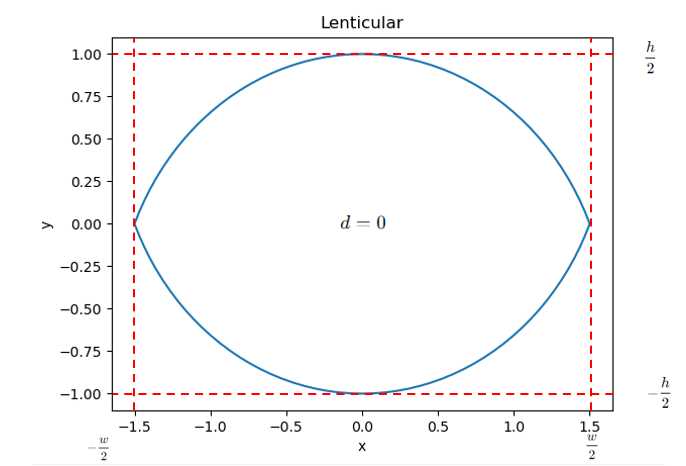
w=10,d=0时,绘制出来的图像
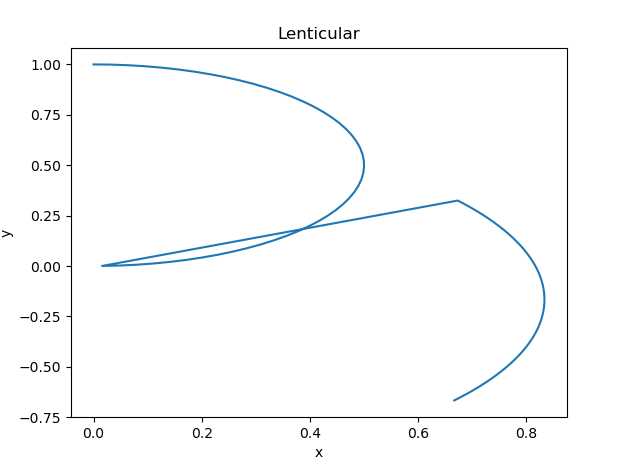
如果根据圆推测公式,x应该对应的是cos,y对应sin,公式变为
$$
C(v)_x=\begin{cases}r_1\cos\theta&0\leq v\leq0.5\\r_2\cos\theta&0.5\leq v\leq1\\\end{cases}\\C(v)_y=\begin{cases}r_1\sin\theta+o_1&0\leq v\leq0.5\\-r_2\sin\theta+o_2&0.5\leq v\leq1\end{cases}
$$
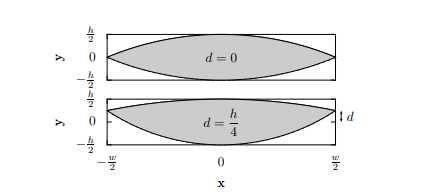
透镜形状横截面图像应为

Comments NOTHING