3.2.1概率转移矩阵的规范形式
寻求一个概率转移矩阵来再现实验数据的两个统计量 RMSD $\sigma_{\xi}^{(w)}$和相关长度 $\zeta_{\xi}^{(w)}(\xi\equiv y\mathrm{~or~}z)$ (经纱的例子)。这两个数据是通过由平稳马尔科夫算子$A$产生的概率分布的渐进行为来实现拟合的。
当$A$多次迭代作用(重复应用$P_{i}^{(n+1)}=AP_{i}^{(n)}$),得到的分布向量逐渐地接近与A的最大特征值相关的$A$的特征向量(任何初始分布向量都可以写成A的特征向量$p_{k}$的线性组合,$A,k=1,\ldots,2m+1$,$P(n)=A^{n}P(0)=\sum_{k=1}^{t}C_{k}\mu_{k}^{n}p_{k}$。当$A$乘以初始向量,线性组合中第$K$个特征向量的系数乘以相应的特征值$\mu_{k}$,如果重复$n$次,则每个系数相乘的因子为$\mu_{k}^{n}$。所以对于较大的$n$, $\mu_{k}$最大的项占主导地位。)设$\mu^{>}$表示最大特征值,$p^{>}$表示相应的特征向量,因为$A$的元素都是正的,列和为1,$\mu^{>}$=1。
证:为什么达到稳态时,$\mu^{>}$=1。
由于$A$的每一列和都为1,所以考虑用$ A-E$ ,显然有:
$$
|A-E|=0
$$
$A-E$相当于$A$的每一列和都减去1,因此$A-E$的每一列和都为0。
$$
|A-E|=\prod_{k=1}^{2m+1}(\mu_{k}-1)
$$
(矩阵特征值之积等于矩阵行列式的值)
于是有
$$
\prod_{k=1}^{2m+1}(\mu_{k-1})=0
$$
所以一定存在特征值为1的情况。且$A$的列和为1,所以
$$
|\mu_{k}|\leq1
$$
即$A$的最大特征值为1,得证。
Markov chain实现的 RMSD 可以用$p^{>}$表示:
$$
\tilde{\sigma}_{\xi}^{(w)}= \sqrt{ \langle \delta \tilde{\xi}^{2} \rangle } \newline =\left[ \frac{\sum_{k}{(ka)}^{2}\Pr \lbrace \delta \tilde{\xi}^{(n,j,w)}=ka \rbrace }{\sum_{k}\Pr \lbrace \delta \tilde{\xi}^{(n,j,w)}=ka \rbrace } \right]^ {1/2}
$$
$\langle \rangle$表示期望值,$\Pr \lbrace {\delta\tilde{\xi}^{(n,j,w)}=ka} \rbrace $ 是 $\delta\tilde{\xi}^{(n,j,w)}$ 在网格点 $(n,j)$ 取离散值 $ka$ 的概率。其中分母$\sum_{k}\mathrm{Pr}{\delta\tilde{\xi}^{(n,j,w)}=ka}$表示在网格点$(n,j)$取离散值$ka$的概率的全部加和,概率和为1。
在马尔科夫过程的稳态状态中,$\mathrm{Pr}{\delta \tilde{\xi}^{(n,j,w)} = ka}=p_{k}^{>}$($p^{>}$中的第$k$个元素)有
$$
\tilde{\sigma}_\xi^{(w)}=a\sqrt{\sum_kk^2p_k^>}
$$
在连续的数据点$\delta\tilde{\xi}^{(n,j,w)}$的值之间实现的相关性为
$$
\tilde{\mathcal{C}}_\xi^{(n,n+1,j,w)}=\langle\delta\tilde{\xi}^{(n,j,w)}\delta\tilde{\xi}^{(n+1,j,w)}\rangle/(\tilde{\sigma}_\xi^{(w)})^2=\left(\frac{1}{\tilde{\sigma}_\xi^{(w)}}\right)^2\frac{\sum_{k,k}kak^{\prime}a\Pr \lbrace(\delta\tilde{\xi}^{(n,j,w)}=ka)\&(\delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a) \rbrace }{\sum_{k,k}\Pr \lbrace (\delta\tilde{\xi}^{(n,j,w)}=ka)\&(\delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a) \rbrace}
$$
$\Pr \lbrace (\delta\tilde{\xi}^{(n,j,w)}=ka)\&(\delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a) \rbrace
$是$\delta\tilde{\xi}^{(n,j,w)}$在沿丝束的连续网格点取离散值$ka$和$k^{\prime}a$的联合概率。
在稳定状态下
$$
\Pr \lbrace (\delta\tilde{\xi}^{(n,j,w)}=ka)\&(\delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a) \rbrace =\Pr \lbrace \delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a|\delta\tilde{\xi}^{(n,j,w)}=ka \rbrace \Pr \lbrace \delta\tilde{\xi}^{(n,j,w)}=ka \rbrace =A_{k^{\prime},k}p_k^{>}
$$
所以
$$
\sum_{k,k^{\prime}}\Pr \lbrace (\delta\tilde{\xi}^{(n,j,w)}=ka)\&(\delta\tilde{\xi}^{(n+1,j,w)}=k^{\prime}a) \rbrace =\mu^{>}\sum_{k}p_{k}^{>}=1
$$
(因为$Ap_{k}=\mu_{k}p_{k}$,在矩阵乘法中,矩阵乘以特征向量等于对应的特征值乘以特征向量,$\mu^{>}$=1,$\sum_{k}p_{k}^{>}=1$,$p_{k}^{>}$一组归一化的概率也为1)。
$$
\tilde{C}_\xi^{(n,n+1,j,w)}=\frac{\langle\delta\tilde{\xi}^{(n,j,w)}\delta\tilde{\xi}^{(n+1,j,w)}\rangle}{(\tilde{\sigma}_\xi^{(w)})^2}=\left(\frac{a}{\tilde{\sigma}_\xi^{(w)}}\right)^2\sum_{k,k}kk^{\prime}p_k^>A_{k^{\prime},k}
$$
根据公式的假设,其独立于网格数$n$或纤维束$j$。所以现在考虑$(2m+1)\times(2m+1)$三对角概率转移矩阵。
$$
A_{0} =\begin{vmatrix} \alpha & \gamma & 0& \cdot & & & & & & \cdot& 0 \\ {\beta}'& \alpha& \gamma & 0& \cdot& & & & & & \cdot \\ 0& \beta& \alpha & \cdot& \cdot& \cdot& & & & & \\ \cdot& 0& \cdot& \cdot& \gamma & 0& \cdot& & & & \\ & \cdot& \cdot& \beta& \alpha & \delta & 0& \cdot& & & \\ & & \cdot& 0& \beta & \alpha & \beta & 0& \cdot& & \\ & & & \cdot& 0& \delta& \alpha & \beta & \cdot& \cdot& \\ & & & & \cdot& 0& \gamma & \cdot& \cdot& 0& \cdot \\ & & & & & \cdot& \cdot& \cdot& \alpha & \beta & 0 \\ \cdot & & & & & & & 0& \gamma & \alpha & {\beta}' \\ 0& \cdot& & & & & & \cdot& 0& \gamma & \alpha \end{vmatrix}
$$
其中所有元素取[0,1]中的值,所有列相加为一。即 $α+β+γ=1$,$α+2δ=1$,$α+\beta^{\prime}=1$。且$A_{0}$具有反转对称性$(A_{k,k^{\prime}}=A_{-k,-k^{\prime}},0\leq k\leq m,0\leq k^{\prime}\leq m)$。
可以把偏差$\delta\tilde{\xi}^{(n,j,w)}$离散到$ \lbrace -ma,-(m-1)a,..,0,...,(m-1)a,ma \rbrace,\mathrm{~with~}ma=3\sigma_\xi^{(w)}$看做是一个生死链过程(birth-death chain),即

如果$A_{0}$被用作生成器,则$\delta \tilde{\xi}^{(n,j,w)}$将在零附近均匀分布。所产生的偏差 $\tilde{\sigma}_{\xi}$(省略了丝束两种类型符号)可以通过改变$\beta$和$\gamma$的相对大小来控制。当$\beta$大于$\gamma$时,在birth-death chain的每一步都倾向于向$\delta\tilde{\xi}=0$靠拢,所以当$\beta - \gamma$从0开始增加时,$\tilde{\sigma}_{\xi}$减小。
在极限$β=γ$时,$β=γ=δ$,birth-death chain变为

如果不考虑边缘离散值m和-m的概率,可以近似看做每个网格点离散到每一个相应值的个数都是不变的且都是相等的,所以$\tilde{\sigma}_{i}$可以取以下近似值
$$
\sigma_{max}=\sqrt{\frac{\sum_{k=-m}^m{(ma)}^2}{2m+1}}=\sqrt{\frac{2\sum_{k=0}^m{m}^2}{2m+1}}a=\sqrt{\frac{2\cdot\frac{1}{6}(m+1)(2m+1)m}{2m+1}}a=\sqrt{\frac{m(m+1)}3}a
$$
$$
1^{2}+2^{2}+3^{2}+\cdots+m^{2}=\frac{m(m+1)(m+2)}{6}
$$
$\tilde{\sigma}_{i}$近似等于$\tilde{\sigma}_{max}$的前提是忽略了边缘离散值m和-m的概率,所以$\tilde{\sigma}_{max}$和$\tilde{\sigma}_{i}$的极限值之间的差异就取决于边缘离散值的概率与中间离散值概率值比$β/\beta^{\prime}$,图3a显示了$\tilde{\sigma}_{\xi}/\sigma_{\max}$的变化,如果 $α$变化,$β$也变化以保持$β/\beta^{\prime}$也就是$\beta/(1-\alpha)$不变那么$\tilde{\sigma}_{\xi}/\sigma_{\max}$也保持不变。$\tilde{\sigma}_{\xi}/\sigma_{\max}$随m的变化不显著,可以通过选择适当的$m$和$a$,找到$β$来达到任何目标的RMSD。
无论 $α$和$β-γ$的值是多少,相关参数$\tilde{C}_{\xi}^{(n,n+1)}$在数值上保持接近1(忽略对丝束类型的引用)。在这里我的理解是参考文章前面的假设(a3)同一丝束上不同点处的分量 $\delta\tilde{\xi}$ 是相关的,相关程度随着点的分离而减弱。相邻两个网格点的相关程度很大,所以相关参数在数值上保持接近1.如果$\alpha\rightarrow1$,$\tilde{C}_\xi^{(n,n+1)}\to1$(也就是在birth-death chain中,不同网格点的离散值保持不变),马尔科夫序列中$\delta\tilde{\xi}$的连续值是完全相关的。随着$α$的减少,$\tilde{C}_{\xi}^{(n,n+1)}$的值略微减小,但是 $\delta\tilde{\xi}$ 连续值的间隔永远不超过a,因此$\tilde{C}_{\xi}^{(n,n+1)}$减小会受到限制。$A_{0}$的三对角形式可以生成任何的RMSD分布,但是不能独立控制相关参数。
因此,考虑概率转移矩阵
$$
A_N=A_0^N
$$
其表示三对角转移矩阵$A_{0}$的$N$个迭代作用,首先要注意的是
$$
A_Np^>=A_0p^>
$$
因为在稳定状态下
$$
A_{0}P^{>}=A_{0}^{N}P^{>}=A_{N}P^{>}
$$
即在稳定状态下,$A_{0}$和$A_{N}$产生相同的 $\delta\tilde{\xi}$ 分布。因此,如果选择$A_{0}$来实现$\tilde{\sigma}_{\xi}=\sigma_{\xi}^{(w)}$ ,那么$A_{N}$也将实现$\tilde{\sigma}_{\xi}=\sigma_{\xi}^{(w)}$ 。但是如果不是在稳定状态下,相关参数$\tilde{C}_{\xi}^{(n,n+1)}$将随着$N$的增加而单调减小。因为马尔科夫链中初始状态分布必须随着每次过渡到新状态而逐渐消失,即$P_{i}^{(n)}\rightarrow A_{0}P_{i}^{(n)}$。即使$α$非常接近1,如果N选择足够大, $\tilde{C}_{\xi}^{(n,n+1)}$也可以减小到零。
3.2.2校准马尔科夫链
首先为离散变量$\delta\xi $创建网格,要求$m$和$a$满足
$$
\sigma_\xi=\frac{ma}3
$$
即允许在实验确定的标准偏差上波动,波动不能超过3个偏差 ,从而使得离散空间$ \lbrace -ma,-(m-1)a,\ldots,0,\ldots,(m-1)a,ma \rbrace $可以代表$\delta\xi $的值。
选择$m=10$,与最可能的数值范围相比,可以确保$\delta\xi $在所允许的离散值之间的间距是相当小的,那么$a$的值就可由上式得出。
如果选择$α=0.9$,则条件
$$
\tilde{\sigma}_{\xi}=\sigma_{\xi}
$$
减小到
$$
f=\frac{m/3}{\sqrt{\frac13m(1+m)}}\approx0.55\quad\text{(for }m=10)
$$
$f(\beta,\alpha)$是图$a$中的函数,这与$\beta+\gamma=1-\alpha $一起决定了$\beta$的值。在设定了$\beta$的情况下,通过要求生成的相关参数$\tilde{C}_{\xi}^{(n,n+1)}$等于实验确定的统计量$C_{\xi}$来确定$N$(如图$b$)。
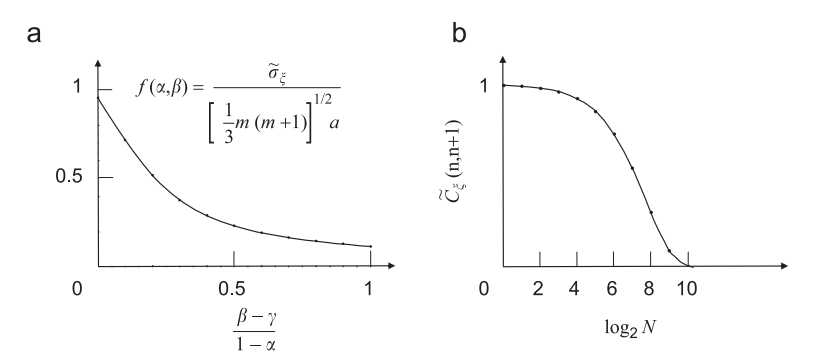
用论文前面2.4中的数据,对每个丝束属重复校准。
3.2.3操作虚拟样本生成器
虚拟样本生成器通过将质心坐标 $(\xi,z)$ 分解为非随机的、周期性变化(系统性变化),再加上随机性的偏差。
$$
(y,z)^{(n,j,w)}=\langle(y,z)^{(n,j,w)}\rangle+(\delta y,\delta z)^{(n,j,w)}
$$
对坐标的系统性变化是通过应用以下方程产生的。
$$
\langle(y,z)^{(nj,w)}\rangle=\boldsymbol{u}_\phi^{(w)}+r\frac{\lambda_x}4\hat{\boldsymbol{x}}+s\frac{\lambda_y}4\hat{\boldsymbol{y}}
$$
通过Monte Carlo生成每根丝束的随机变化。生成器生成的随机坐标的统计数据对于任何丝束上的所有统计点都应该是统一的。在纤维的开始处不应该存在马尔科夫过程的结果逐渐向稳态分布$p^{>}$过渡,因为Monte Carlo是基于马尔科夫链平稳分布的对应样本集进行采样的。可以通过从分布$p^{>}$中选择丝束上第一个点的随机坐标值来保证样本集均是平稳分布的。当在许多副本上采样时,通过应用概率转移矩阵为丝束上的后续点生成的坐标值集合将具有相同的分布。
Monte Carlo方法的实现涉及以下从概率分布向量导出的分段常数函数,
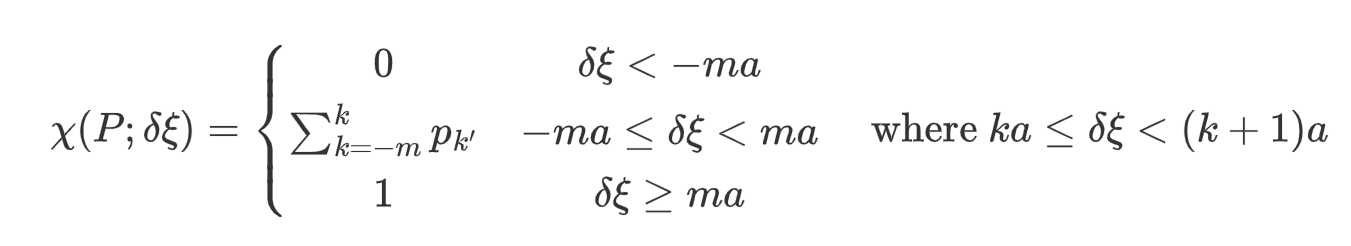
在这里我的理解是$\delta\xi $在这里应该是最大的离散值,当 $\delta\xi<-ma$,概率为0;当 $-ma\leq\delta\xi};ka)\leq\eta};(k+1)a)
$$
$$
\delta\tilde{\xi}(1,w)=ka
$$
对于来自离散集合$\ \lbrace -ma,-(m-1)a,..,0,..,(m-1)a,ma\ \rbrace $的丝束上的第一个点$(1,w)$的值为$ka$,记作$k_{1}a$ 。
3.通过以下迭代的方式填写纤维束上剩余点的$\delta\tilde{\xi}$值。
给定$\delta\tilde{\xi}$在第n个网格点的值$k_{n}a$定义分布向量
$$
\pi_i^{(n)}=\mid\mathbf{0}\quad\ldots\quad\mathbf{0}\quad\mathbf{1}\quad\mathbf{0}\quad\ldots\quad\ldots\quad\mathbf{0}\mid^T
$$
其中非零元素出现在$n$处。
4.形成概率分布向量
$$
P_i^{(n+1)}=A\pi_i^{(n)}
$$
然后选择另一个随机数 $\eta $,并通过 $\eta $与$\chi(P_{i}^{(n+1)};\delta\xi)$ 比较来确定$\delta\tilde{\xi}(n+1,w)$ ,类似步骤2,值记作$k_{n+1}a$ 。在$n+1$处形成一个非零元素的向量 $\pi_{i}^{(n+1)}$,类似步骤3。
5.重复步骤4直到丝束上的点全部被填充完毕。
因为分布向量$\pi_{i}^{(n)}$只有一个非零项,所以$P_i^{(n+1)}=A\pi_i^{(n)}$4是一个微不足道的替换,而不是矩阵乘法,实现操作虚拟样本生成器花费的计算工作量非常小。
3.3消除网格效果
马尔科夫链算法以与目标RMSD和相关长度一致的方式成功地再现了沿纤维束轴变化的随机坐标偏差。
图中显示了随机偏差(中心纬纱丝束的)的典型实例。大振幅、长波长变化发生在沿丝束的距离上,该距离与目标相关长度$\zeta_{x}^{(cw)}$相当。然而,该马尔科夫链算法也会产生小幅度、短波长的振荡,这些振荡在原始生成的曲线上表现为尖锐的随机尖峰(也就是图中的细线)。尖峰的振幅可以通过细化随机变量的网格来减小(增加离散值的$m$,但是要同时保持$ma=3\sigma_{x}$),并且尖峰的波长取决于沿丝束的网格密度。因此尖峰是依赖于网格的。
但是这些尖峰是不现实的,因为连接的丝束不可能在其位置上表现出如此强烈的变化。尖峰是由于假设偏差被视为马尔科夫过程计算产生的。在图中的例子,网格点$k$处的值$\delta x_{k}$仅取决于网格点$k-1$处的$\delta x_{k-1}$,而不取决于网格点$k-2$处的$\delta x_{k-2}$。马尔科夫链生成器没有模仿连续纤维保持平滑倾向的约束。
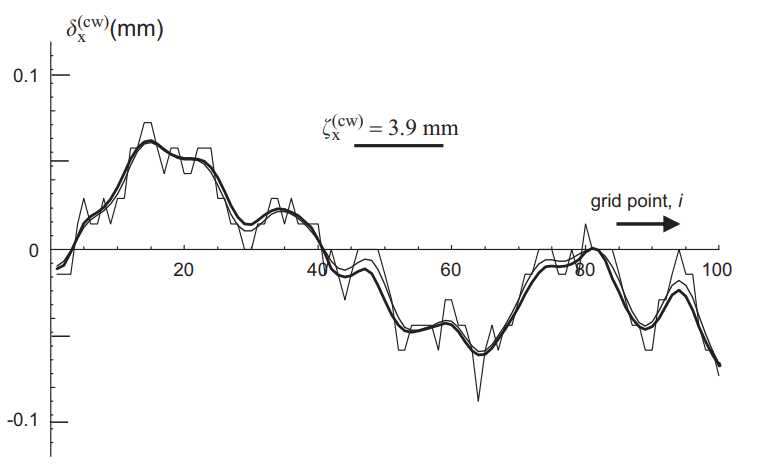
可以通过对生成的偏差序列应用局部平均来平滑尖峰。为了最大限度地减少其对生成偏差的RMSD的影响,使用新制定的算法对偏差的平方进行平均。
$$
\chi_{i}^{(s)}=S\sqrt{\frac{1}{2m+1}\sum_{j=-m}^m\chi_{i+j}^2}
$$
上标$s$代表平滑的量, $\chi$表示偏差,等式中的$S$是符号因子,因为偏差有正负,而取平方根的结果是非负的,所以取$S$来表示偏差的正负。该等式仅适用于平均区间内所有$\chi_{i}$具有相同的符号或者为零的情况,非零项的符号就是$S$的符号。当平均区间内穿过$\chi=0$时,该等式不适用。
对于 $\chi_{i}$中包含符号变化的区间,使用公式常规平均规则。
$$
\chi_{i}^{(s)}=\frac{1}{2m+1}\sum_{j=-m}^m\chi_{i+j}
$$
等式$\chi_{i}^{(s)}=S\sqrt{\frac{1}{2m+1}\sum_{j=-m}^m\chi_{i+j}^2}$在偶尔出现平均区间$\chi=0$穿过零的情况下也能最大程度地减少平滑对生成偏差的RMSD的影响。在马尔科夫链算法产生的偏差中,穿过零的情况相对不多,因为与偏差的相关长度相比,网格是密集的,而且在零附近的元素对RMSD的影响很小。
为了避免影响丝束的相关性,在小于偏差的基准相关长度的标距长度进行平均。细平滑曲线是对偏差序列应用常规平均规则平滑的结果,粗平滑曲线是应用新制定的算法对偏差的平方进行平滑的结果。对于每个平滑过程,使用±4个网格间隔的加权信息递归平滑操作,从而合并了在任意网格点i到网格点i±4的加权信息。
粗曲线所示:物理上显著的大振幅、长波长变化保持不变,而非物理的尖峰则减少到振幅非常小(几毫米)的波纹,对复合材料的预测机械性能的影响可以忽略不计。

Comments NOTHING