Please refresh the page if equations are not rendered correctly.
---------------------------------------------------------------
Variance
Could use any measure of dispersion.
- Variance
- Population variance average squared difference from the mean
\sigma^{2}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}
- Unbiased estimate of population variance from sample set
s^{2}=\frac{1}{N-1} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}
- Standard Deviation
\sigma=\sqrt{\sigma^{2}}
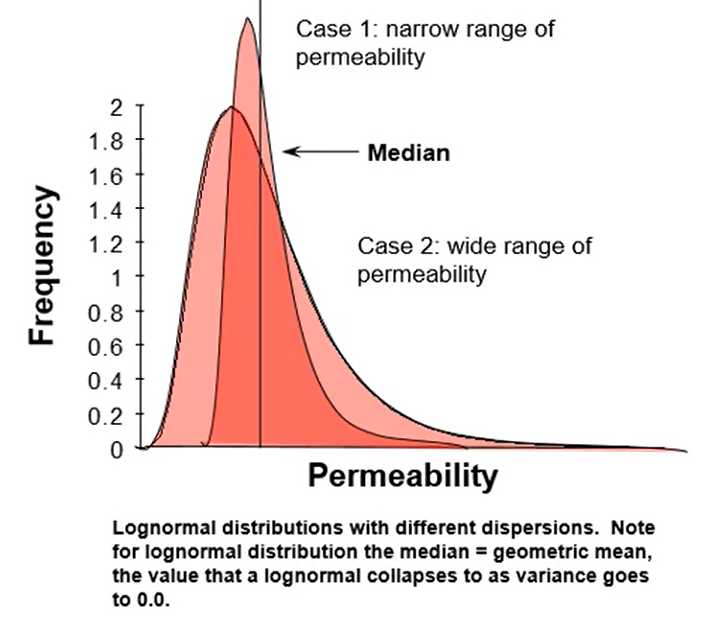
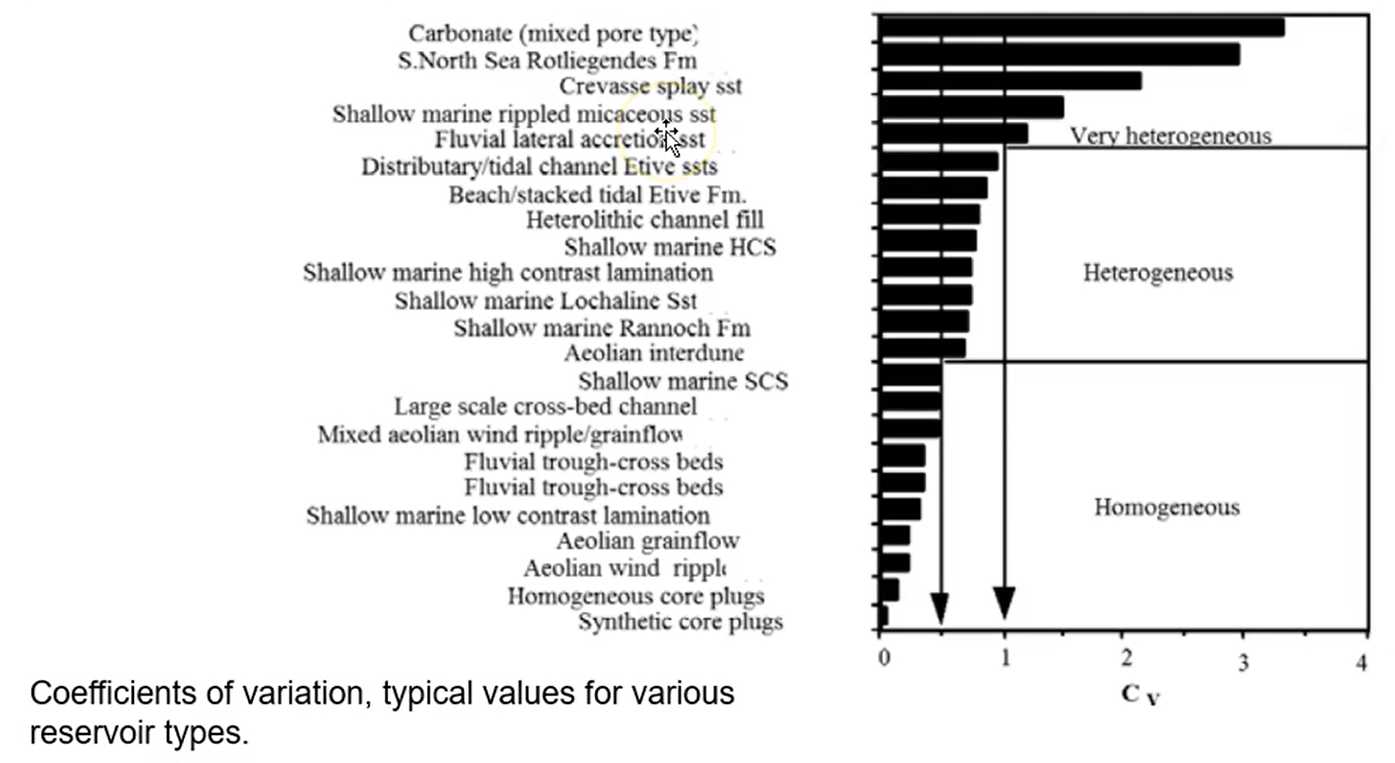
Dykstra-Parsons Coefficient of Variation
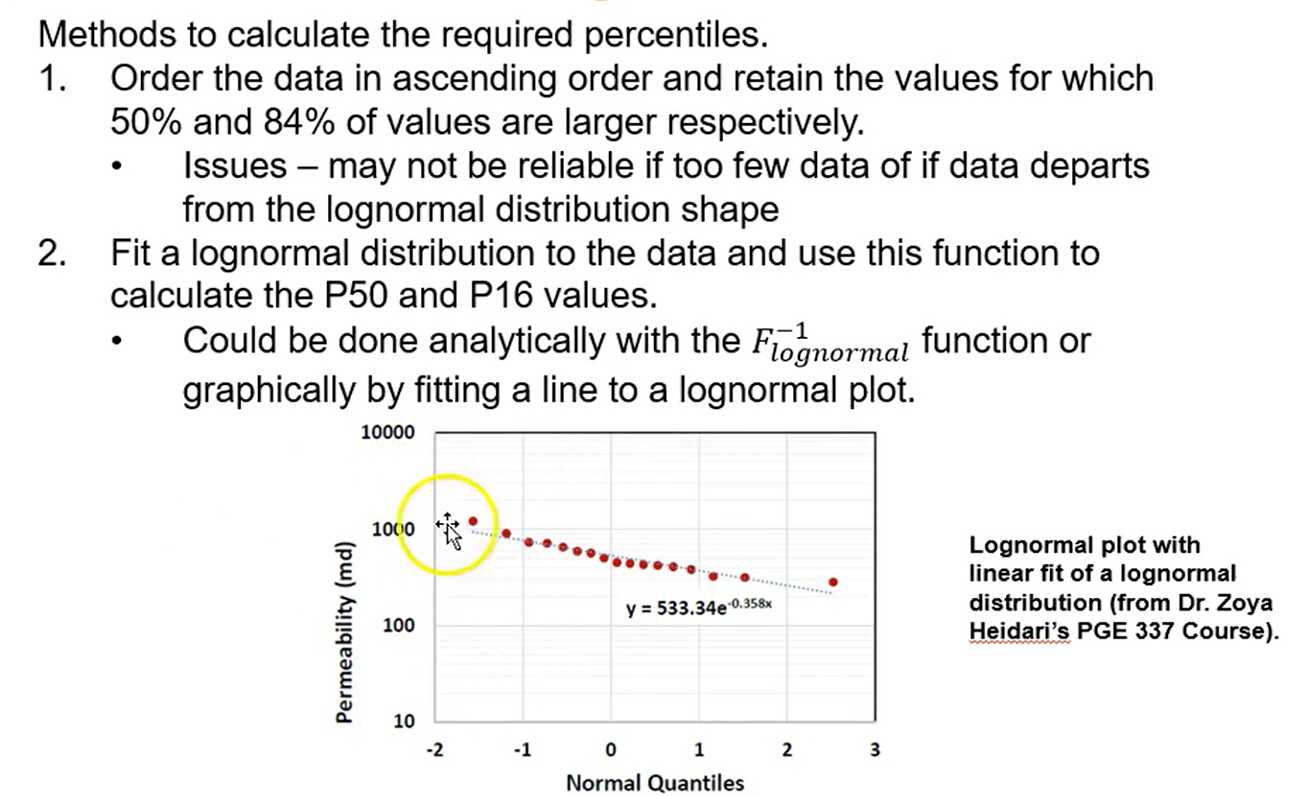
Dykstra-Parsons Coefficient of Variation is a popular method for assessment of permeability variation:
Consider end members:
If \sigma_{k}^{2}=0 then k_{50}=k_{16} and V=0.0
V \leq 1.0 since k_{16} \geq 0.0
Lorenz Coefficient
https://youtube.com/clip/UgkxKLFthw1KyOQQCa_eV2SmEHucEcbVvUu0
Comments NOTHING